nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber101.
- CommentAuthorDavidRoberts
- CommentTimeMar 30th 2010
Not that I know of. -
- CommentRowNumber102.
- CommentAuthorEric
- CommentTimeMar 30th 2010
Hmm. Maybe I'll consider it homework. It seems intuitive enough.
-
- CommentRowNumber103.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
It is covered in chapter 1.1 of HTT by Lurie.
A category is a simplicial set such that every inner horn has a unique filler.
Defining it that way is quite circular, though.
-
- CommentRowNumber104.
- CommentAuthorDavidRoberts
- CommentTimeMar 30th 2010
Not necessarily. A simplicial set is just a sequence of sets and a bunch of maps. If you want to define it as a presheaf on Delta, then go ahead, but it isn't necessary. -
- CommentRowNumber105.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Information about "Grothendieck's results" (if that's what you call it) about characterization of simplicial sets that arise as nerves of categories is at
Eric's intuition that "categories should be built just using triangles" is made precise by the fact that the nerve of every category is a 2-coskeleton. That means it is determined by a truncated simplicial set that has just objects, edges and triangles.
-
- CommentRowNumber106.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Is there anything remotely close to a reference for "scientists and engineers" that explains Grothendieck's results regarding simplices?
Not sure about references, but if you understand functors, you are up to understanding morphisms of simplicial sets. In fact, you have already discovered parts of it yourself.
I added a few remarks on how functors are equivalently morphisms of simplicial sets between nerves of categories at functor (search for "nerve").
I can recomment to you
- Greg Friedman, An elementary illustrated introduction to simplicial sets
I expect that you would enjoy this.
-
- CommentRowNumber107.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
-
- CommentRowNumber108.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
[quick note]
I like the opening paragraphs in Friedman. Although I started from a much lower base, those same references, and references on simplicial sets in general, seemed grossly un-geometrical for something so completely geometrical.
[/quick note]
[PS]
His pictures remind of Section 3.4 in my dissertation :)
[/PS]
-
- CommentRowNumber109.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Hey, Eric. Do you still go to Efnet-#math? I know all of the people you're talking about in the intro to your dissertation.
-
- CommentRowNumber110.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
EFNet-#math still exists?!?!? :)
And those guys are still there?!??! :)
I haven't been there in 10 years, but was a regular. Do they still have "ops"? I was an "op" on #physics, #mathematics, and #math for many many years :)
-
- CommentRowNumber111.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Uh, could you get me unbanned from efnet-#math? =)
Anyway, Polytope and Galois are still there. Nerdy2 has disappeared somewhat though. He's writing his dissertation or something.
-
- CommentRowNumber112.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
I should hire someone to LaTeX-ify "Simplex-"es thesis. It remains the most beautiful piece of science I have ever read. He was a student of Charles Misner, but retreated from the rat race that is science and happily teaches at a community college. The physics community lost this sleeping giant :)
-
- CommentRowNumber113.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Uh, could you get me unbanned from efnet-#math? =)
I can't imagine how you could have managed to get yourself banned from #math :D
By the way, I met Galois in "meat space" after knowing him for years online while I was working MIT.
My wife and I visited Polytope a few times in Wisconsin. Crazy :)
-
- CommentRowNumber114.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
Not banned, just silenced. I mean, you know, it's the whole thing about calling stupid questions stupid or purposely giving the wrong answer.
Like for example:
:::: (05:37:40) :::: ( idiot ) wut is the mean of (insert long URL that links to a large list of numbers)? I can't do it I need help.
:::: (05:37:40) :::: ( fpqc ) What a stupid question. The answer is obviously 99999999999999999999999999999999999999999. Can't you count? -
- CommentRowNumber115.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Interesting. So what you guys call a 2-simplex is precisely the drawing of a commuting triangle, i.e. one edge is singled out and the other two are effectively "composites". A horn is a lot like an outer oriented
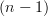 -simplex embedded in the boundary of an
-simplex embedded in the boundary of an  -simplex (see pdf-page 39 of my dissertation).
-simplex (see pdf-page 39 of my dissertation).Edit: This makes me want to say, "a category is an outer oriented simplicial complex". Or something...
-
- CommentRowNumber116.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
It's kind of funny. I feel like I'm cheating because I've been following Urs and everyone here on the n-community so long, I vaguely know where the story is taking me.
It's basically something like Kan complex

 -groupoid.
-groupoid.It's pretty obvious the degeneracy maps are identity-assigning morphisms, right?
This is related to what I have talked about in the past (and not sure I made much sense back then either) that there is always a 2-morphism spanning any triangle. If the diagram commutes, this 2-morphism is an identity morphism. So a 2-morphism measures the failure of a 1-diagram to commute.
Now consider a simple example consisting of a single object with only identity morphisms.
If we perform Urs' trick and draw the object three times and draw three identity morphisms (which are really the same but we are playing Urs' game again) forming a triangle, then as I said, there is a 2-morphism across it. Of course the diagram commutes, so this 2-morphism is an identity 2-morphism.
Bumping things up a dimension, we can say that for any 3-simplex, there is a 3-morphism spanning two opposite 2-simplices. If this 2-diagram commutes, it means the 3-morphism is an identity morphism.
If we return to our game and add a forth copy of the single object forming a degenerate 3-simplex, then obviously the 3-simplex commutes since it is made entirely of identity 1- and 2-morphisms, then we have an identity 3-morphism.
Etc etc etc.
So already a single object is an
 -groupoid consisting of all degenerate commuting
-groupoid consisting of all degenerate commuting  -simplices for
-simplices for 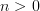 .
.Some of what Urs has been saying for years is starting to make sense to me now :)
-
- CommentRowNumber117.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
What you said near the end is almost the right idea, but the rest of it isn't really.
-
- CommentRowNumber118.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Wait and see :)
I am pretty sure I've got the basic concept correct even if stated in an unorthodox way. I'll try to find our earlier discussion.
Edit: Found it. See the discussion at finite category.
-
- CommentRowNumber119.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
Well, in the infinity-case you can't reduce everything to 2-dimensions is the point.
-
- CommentRowNumber120.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
So what you guys call a 2-simplex is precisely the drawing of a commuting triangle, i.e. one edge is singled out and the other two are effectively "composites"
Yes, that's the way to think about it. See also the discussion at How to think of a Kan complex as an oo-groupoid
It's basically something like Kan complex
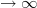 -groupoid.
-groupoid.Yes, you can vary a bit the assumptiions on which triples of morphisms have 2-simplices with them as boundary,m and that will change the notion of what kind of structure exactly you have: a category, a groupoid, an oo-category, an oo-groupoid, etc.
It's pretty obvious the degeneracy maps are identity-assigning morphisms, right?
Yes. That's exactly right.
there is always a 2-morphism spanning any triangle. If the diagram commutes, this 2-morphism is an identity morphism. So a 2-morphism measures the failure of a 1-diagram to commute.
That's morally true, but it may also happen that there is no 2-simplex at all in betweem three given edges in your simplicial set. For instance in a category, if the third edge is not the composite of the incoming two edges, then there is simply no 2-simplex of that sort.
If we perform Urs' trick and draw the object three times and draw three identity morphisms (which are really the same but we are playing Urs' game again) forming a triangle, then as I said, there is a 2-morphism across it. Of course the diagram commutes, so this 2-morphism is an identity 2-morphism.
You could also consider the case where that 2-morphism between identity 1-morphisms is not itself an identity, but a nontrivial 2-automorphism of the identity 1-morphisms. For instance in the 2-groupoid called
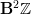 there is one such 2-morphism for each integer number. One of them, of course, is the identity.
there is one such 2-morphism for each integer number. One of them, of course, is the identity.So already a single object is an
 -groupoid consisting of all degenerate commuting
-groupoid consisting of all degenerate commuting  -simplices for
-simplices for 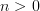 .
.Yes. Generally, every set may be regarded as a discrete groupoid. Even more generally: every n-categgory is also an (n+1)-category. A set is a 0-category and a 0-groupoid.
-
- CommentRowNumber121.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
@Eric: You need to define what you mean by the commutativity in all degenerate cases. I checked the page, and there was no discussion of what it means for any sort of degenerate (not only loop) diagram to commute. I can think of a huge number of degenerate cases for which "commutativity" is not defined. I think that this is stretching the meaning of commutativity too far. If you disagree and insist on using that definition, please add references in the article on commutativity before rolling back the deletion I made. As it stands, it is too confusing.
-
- CommentRowNumber122.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Thanks Urs.
When I wrote my last comment, I originally had said there was a 2-morphism spanning every pair of parallel morphisms, but then remembered that David said triangles were the important shape and changed it at the last minute. While sleeping (I do most of my best work while sleeping :)), I realized that I really do want to say "2-morphism spanning every pair of parallel morphisms".
In the example you gave where the one morphism was not the composite of the other two, the other two (obviously) form a composite, so for every triangle we have two parallel morphisms. The 2-morphism I'm talking about goes between these two.
You could also consider the case where that 2-morphism between identity 1-morphisms is not itself an identity, but a nontrivial 2-automorphism of the identity 1-morphisms.
Ack! Ok. I need to think about this example. It means my idea is not correct after all :)
Identity 1-morphisms obviously form a commuting diagram (right?) so if there is a non-identity 2-morphism between identity 1-morphisms, then that kills the idea. Oh well :)
@Harry: Thanks. Actually, your note might give me a way out. We haven't yet really defined what it means for "higher" diagrams to commute. Maybe.
-
- CommentRowNumber123.
- CommentAuthorEric
- CommentTimeMar 31st 2010
@Harry: You removed my diagrams from functor??!?!?! How dare you??!?!
-
- CommentRowNumber124.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
They did not make sense outside of the context of this conversation!
Add your definitions to commutative diagram, then link to them from the page, because it was too hard to make anything of it without the context of our conversation on the forum!
-
- CommentRowNumber125.
- CommentAuthorDavidRoberts
- CommentTimeMar 31st 2010
For a 1-category, a 2-morphism is an equals sign and only an equals sign. One doesn't need any higher dimensional simplices (i.e 3-dim and above) at this level. Let us walk before we try to run... -
- CommentRowNumber126.
- CommentAuthorEric
- CommentTimeMar 31st 2010
@Harry: Urs saw what I wrote and LIKED it. He added material to it to make it better.
Instead of DELETING EVERYTHING I ADDED, why don't you ADD STUFF TO MAKE IT BETTER?!??!
I absolutely just rolled it back.
-
- CommentRowNumber127.
- CommentAuthorEric
- CommentTimeMar 31st 2010
Hi David. I started to think that a 1-category with non-commuting diagrams was secretly a 2-category with non-identity 2-morphisms spanning the non-commuting diagrams. If any two such 2-morphisms are parallel and do not commute, then we secretly have non-identity 3-morphisms, etc etc.
But Urs' example kills this idea, so I need to think about his example before trying to make sense of that last sentence. There is a high chance it is nonsense so no need to get distracted until I can either make a better argument or give up :)
-
- CommentRowNumber128.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
@Harry: For example, if there is something that bugs you, add a comment like "The following material needs to be fixed. It is not quite right." Don't just delete all my effort.
Or something like, "The following material requires a refinement of commutative diagram such that a "commuting loop" is always an identity morphism." Or something...
The point is to add. Don't take away from the nLab.
-
- CommentRowNumber129.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
There is a whole lot more that you need to develop over there. You need to define what it means for a degenerate diagram to commute.
-
- CommentRowNumber130.
- CommentAuthorEric
- CommentTimeMar 31st 2010
You need to define what it means for a degenerate diagram to commute.
Sure. So let's give it a try :)
Gotta run for now though...
-
- CommentRowNumber131.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
<p>Ok. Almost literally had a EUREKA! moment, but decided to finish my shower before coming back here :)</p> <p>I'm sure again that this simple idea can be made precise. The secret is to relate commuting higher diagrams to the discussion at:</p> <p><a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=723&page=1">is every connection flat?</a></p> <p>Just as every (higher) connection is flat, all (higher) diagrams commute. The latter statement is actually more general than the first, since the first applies only to groupoids and the latter applies to any <img src="/extensions/vLaTeX/cache/latex_bbcfc94cb45a046c5a7c9e0d8e4e8681.png" title="(\infty,n)" style="vertical-align:-20%;" class="tex" alt="(\infty,n)" />-category .</p> <p>If a 1-diagram does not commute, it implies the existence of a non-identity 2-morphism. In the example Urs gave, that non-identity 2-morphism means the 1-diagram of identity 1-morphisms does not commute. No big deal.</p> <p>To make this precise, we should create an nPOV page for <a href="https://ncatlab.org/nlab/show/commutative+diagram">commutative diagram</a>.</p> <p>A first attempt (which is probably wrong) would be along the lines, "An <img src="/extensions/vLaTeX/cache/latex_485d65c1e6e7757e4de10eb91bc9382b.png" title="n" style="vertical-align:-20%;" class="tex" alt="n" />-diagram commutes if there is no non-identity <img src="/extensions/vLaTeX/cache/latex_c453a3095393fbd3d3aa086ede9925ec.png" title="(n+1)" style="vertical-align:-20%;" class="tex" alt="(n+1)" />-morphism spanning it."</p> <p>This is similar to saying, "An <img src="/extensions/vLaTeX/cache/latex_485d65c1e6e7757e4de10eb91bc9382b.png" title="n" style="vertical-align:-20%;" class="tex" alt="n" />-connection is flat if all <img src="/extensions/vLaTeX/cache/latex_c453a3095393fbd3d3aa086ede9925ec.png" title="(n+1)" style="vertical-align:-20%;" class="tex" alt="(n+1)" />-holonomies (or holonomoids? :)) are trivial." Or something...</p> <p>Gotta catch my train now...</p> -
- CommentRowNumber132.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
No, you're definitely overthinking it.
Or rather, throwing a bunch of irrelevant machinery at it.
-
- CommentRowNumber133.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Note: I'll leave this here to record my thought, but please ignore the attempt below. It is not correct. The first attempt above is better.
A second attempt...
"An
 -diagram commutes if all
-diagram commutes if all 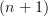 -morphisms spanning it are invertible."
-morphisms spanning it are invertible."Not sure if I like this one or not though...
-
- CommentRowNumber134.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Eric, Harry,
those diagrams at functor are good, certainly the first one is. It is true that in in practice one rarely speaks of the commutavity of a loop diagram, instead one does draw out explicitly the identity morphism that is otherwise hidden, to remove ambiguityy.
Instead, people often draw loops that are not supposed to "commute", i.e. not supposed to be the identity morphism. But that still does not mean that it would not make good sense to speak of "loops that do commute".
I suggest: leave the diagrams there (they are exactly the right way to visualize a functor!), but add a remark to the second one about what exactly it is supposed to mean that a "loop commutes". Namely that starting at any object and going around the loop produces the identity morphism.
@Harry: the established practice here is that when you have a quarrel with material at an entry, you drop a query box there (you know how to do this?) in which you voice the complaints. This way the material is marked to other readers as potentially controversial, and other people have a chance to add their comments to the controversey. Typically eventually a genuine consus emerges and the entry improves in the long run.
There is a whole lot more that you need to develop over there. You need to define what it means for a degenerate diagram to commute.
I don't understand, what is the problem here? The standard definition is that a diagram commutes if all possible ways to go from any given object in the diagram to any other given object are equal. With that standard definition, Eric's definition of commuting loop is precisely correct.
Let's have a page on commuting diagrams.
Just as every (higher) connection is flat, all (higher) diagrams commute.
For that discussion of connections, the point was that one can take care to use an oo-groupoid with the special property that all n-morphisms between given (n-1)-morphisms exist. But this is not in general so.
Just like with morphisms: not between every given pair of objects need there be a morphism. Similarly, not between every given pair of parallel morphisms need there be a 2-morphism. As David said: in a 1-category every 2-morphism is an identity, and certainly not every parallel pair of 1-morphisms needs to be equal.
-
- CommentRowNumber135.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
<p>@Urs: My point was more along the lines of: What does it mean for the following diagram to commute:</p> <img src="/extensions/vLaTeX/cache/latex_9f9d6778fe16a52be19b2c6fb06ca943.png" title="A\stackrel{\rightrightarrows}{\rightrightarrows}B" style="vertical-align:-20%;" class="tex" alt="A\stackrel{\rightrightarrows}{\rightrightarrows}B" /> <p>I mean, there are all of these stupid degenerate cases of commutativity.</p> <p>Also, if you just say what you said about the loops, then consider the stupid case where you have a nontrivial idempotent endomorphism. you can expand the loop diagram out to a diagram where all of the morphisms are the idempotent, in which case the extended diagram</p> <img src="/extensions/vLaTeX/cache/latex_ca08b5007d5733d771ec1226efc6f6bd.png" title="\begin{matrix}&&e&&\\ &x&\to& x&\\ &e\searrow & &\swarrow & e\\ &&x&& \end{matrix}" style="vertical-align:-20%;" class="tex" alt="\begin{matrix}&&e&&\\ &x&\to& x&\\ &e\searrow & &\swarrow & e\\ &&x&& \end{matrix}" /> <p>commutes when <img src="/extensions/vLaTeX/cache/latex_9aaa2c2772d8ae53e9d59b54be9712fc.png" title="e" style="vertical-align:-20%;" class="tex" alt="e" /> is a nontrivial idempotent. A loop being "commutative" is the wrong notion then. What we really want to say is that the loop is contractible.</p> <p>That is, we want the diagram</p> <img src="/extensions/vLaTeX/cache/latex_22702edcff06845b1492f1e199052fb0.png" title="\begin{matrix}&&e&&\\ &x&\to& x&\\ &id_x\searrow & &\swarrow & id_x\\ &&x&& \end{matrix}" style="vertical-align:-20%;" class="tex" alt="\begin{matrix}&&e&&\\ &x&\to& x&\\ &id_x\searrow & &\swarrow & id_x\\ &&x&& \end{matrix}" /> <p>to commute.</p> <p>Which one of these you mean is not a priori clear by just saying "the loop commutes".</p> -
- CommentRowNumber136.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Harry, as I said: a diagram commutes if all possible ways to go between any given ordered pair of objects are equal.
Apply this to your three examples to get the answer:
the first diagram commutes if all these morphisms between A and B are equal. Draw the arrows slightly curved to recover your intuition about commuting diagrams!
The second diagram commutes precisely if e is an idempotent, yes. It is not a "loop diagram" of the sort we have been discussing.
Finally the last diagram, which is different, commutes precisely if e is the identity. You may discard drawing the two identity arrows here, since these need not be drawn, and then you find Eric's notion of a commuting loop which says that its morphism is an identity.
I urge you to think about the definition: a diagram commutes if all possible ways to go between any given ordered pair of objects are equal.
-
- CommentRowNumber137.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
@Harry: Your first diagram with the nontrivial idempotent does not commute. Although it semicommutes :)
There are actually three more loops, one identity loop for each object
 . To say that diagram commutes means to say that
. To say that diagram commutes means to say that 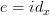 .
.Your second diagram demonstrates this nicely.
Edit: A diagram, must itself be a subcategory, so we rarely draw identities, but they are always there. So when we say a diagram commutes, we have to keep these in mind.
-
- CommentRowNumber138.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
The second diagram commutes precisely if e is an idempotent, yes.
Oh no! I disagree with Urs. What are the chances I'm correct? :)
If a diagram is a subcategory, you can't just forget the identity loops, so I would say Harry's idempotent diagram does not commute although it is interesting. Harry has been working on "semi" pages, so I propose to describe the idempotent situation a "semicommuting diagram".
-
- CommentRowNumber139.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
@Eric: A diagram (Read: The image of a diagram) does not have to be a subcategory. That is not true without using the definition of a functor!
You're not using a standard definition of commutativity. My diagram does commute (when
 is idempotent) in every standard sense of the word.
is idempotent) in every standard sense of the word.@Urs: Then you need to spell out the definition of a loop diagram for me, because it is not obvious what you mean. Any loop can just be written as
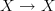 !
!Perhaps you mean for "loop diagram" to mean something different than "loop", because any endomorphism of
 has an image equal to a loop in the underlying graph.
has an image equal to a loop in the underlying graph. -
- CommentRowNumber140.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
I am puzzled about what you guys are puzzled about. Once more:
A diagram commutes if all composites of morphisms in it with the same source and target vertex are equal. Do you understand what I mean by this sentence?
If the diagram
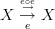 commutes, then this says that
commutes, then this says that 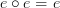 .
.If in a diagram there is a morphism
 going from one vertex
going from one vertex  to itself. Then this has to be equal to the identity morphism on that vertex. It is the same as saying that
to itself. Then this has to be equal to the identity morphism on that vertex. It is the same as saying that 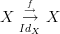 commutes.
commutes. -
- CommentRowNumber141.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
because any endomorphism of X has an image equal to a loop in the underlying graph.
So an arbitrary endomorphism gives a loop diagram, but not necessarily a commuting loop diagram.
-
- CommentRowNumber142.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
I can't see where you're coming up with this map
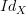 that you keep putting in all of your diagrams.
that you keep putting in all of your diagrams.If I draw the diagram
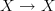 , this has one morphism and is the exact same thing as a loop. Then this diagram commutes because any path we take is equal to any other path we take (there is only one, so this is vacuous).
, this has one morphism and is the exact same thing as a loop. Then this diagram commutes because any path we take is equal to any other path we take (there is only one, so this is vacuous).If you're saying that a loop diagram implicitly has
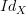 in it, then this can't be taken for granted unless we defined a functor in the first place, in which case it is necessary that diagram, which is itself a functor, maps identities to identities. However, this is circular reasoning.
in it, then this can't be taken for granted unless we defined a functor in the first place, in which case it is necessary that diagram, which is itself a functor, maps identities to identities. However, this is circular reasoning. -
- CommentRowNumber143.
- CommentAuthorEric
- CommentTimeMar 31st 2010
@Urs: I think we all agree on what "commute" means, but we disagree about what "diagram" means.
I think any diagram contains identity loops at each object although we rarely ever draw them. They are there.
Harry disagrees and thinks a diagram need not contain identities.
If Harry's first diagram with idempotents contains hidden identity loops, then declaring the diagram commutes means
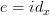 . If there are no hidden identities, then to say the diagram commutes means only that
. If there are no hidden identities, then to say the diagram commutes means only that 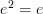 .
.Put another way, I think a diagram should be a subcategory. Harry disagrees.
As a kind of middle road, I proposed to use "semicommute" or maybe "semidiagram" for a diagram without identity loops. This way, I would describe Harry's diagram as "the semidiagram commutes" or something like that.
-
- CommentRowNumber144.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
No, my diagram commutes regardless of whether or not we draw the identities (so long as e is idempotent)...
The problem here is that the standard definition of a diagram is as a functor (or a morphism of graphs into the underlying graph). We have to be extremely careful with our definition of a diagram withoout a pre-existing notion of a functor.
If we allow a diagram to just be any connected directed piece of the underlying graph, then we run into lots of problems.
-
- CommentRowNumber145.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
I have to run now. Notice that in a diagram the vertices matter, not just their labelling by an object.
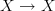 is not a loop diagram, as the morphism goes between two different vertices.
is not a loop diagram, as the morphism goes between two different vertices. -
- CommentRowNumber146.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Sorry sorry! I thought you were drawing loops! Edit: Sorry sorry for apologizing. It doesn't matter whether you were drawing loops or triangles :)
-
- CommentRowNumber147.
- CommentAuthorEric
- CommentTimeMar 31st 2010
Notice that in a diagram the vertices matter, not just their labelling by an object.
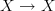 is not a loop diagram, as the morphism goes between two different vertices.
is not a loop diagram, as the morphism goes between two different vertices.Say what?!?!?!?
How can that NOT be a loop diagram??? I thought that was just a curious notations of yours for writing a loop.
-
- CommentRowNumber148.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
There is nothing curious about that notation. For X a set and f a function from the set to itself, they teach in school that this function goes
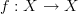 .
. -
- CommentRowNumber149.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
Ah, I get it now, but calling it a commuting loop is really nasty.
The trick is that if we have a loop, we can take the constant path or the path along the morphism. Since the constant path is the identity, a loop is rigged to be the identity if it commutes.
This definition relies on us allowing length-0 paths. What a mess.
To use this definition, however, we need to define a diagram differently, since a diagram is a functor by definition.
-
- CommentRowNumber150.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
There is nothing curious about that notation. For X a set and f a function from the set to itself, they teach in school that this function goes
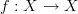 .
.In school, I always pictured it as a loop. As I do now :)
It IS a loop :)
I guess we really do need to establish some conventions. Or if conventions are already established (which is likely) we should write them down. I made a stub at commutative diagram.
-
- CommentRowNumber151.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
This is a huge waste of time and effort to define something in a more abstruse way. If you've seen a group homomorphism, you understand functors. If you don't understand group homomorphisms, go back, read about them, then go back to reading about functors.
-
- CommentRowNumber152.
- CommentAuthorEric
- CommentTimeMar 31st 2010
@Harry #149
Yep yep. That is exactly this issue. I drew a diagram at alternative experimental definition of commutative diagram, but I suppose it is not necessary now.
-
- CommentRowNumber153.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
The risk of circularity is higher than anyone is admitting, since the definition of a diagram depends on either functors or the forgetful-free adjunction (which is functorial as well).
Eric, your diagram is still wrong (arrows are pointing in the wrong direction), and my diagram with the idempotents does in fact commute.
The trick with loops is that you've literally got one arrow from
 to itself curling around. Now, if you try to split X upinto a standard diagram, you have an identity morphism attached, so you end up with a 1-globe that commutes.
to itself curling around. Now, if you try to split X upinto a standard diagram, you have an identity morphism attached, so you end up with a 1-globe that commutes. -
- CommentRowNumber154.
- CommentAuthorEric
- CommentTimeMar 31st 2010
@Harry: For the time being, we can forget about any alternative definitions and just think of diagrams in the traditional sense.
Even then I need to meditate over what Urs said...
-
- CommentRowNumber155.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Uh, the standard definition of a diagram involves functors.
-
- CommentRowNumber156.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
The trick is that if we have a loop, we can take the constant path or the path along the morphism. Since the constant path is the identity, a loop is rigged to be the identity if it commutes.
Yes!
What a mess.
Are you aware that if you complain in every single comment of yours, we will all tend to ignore each and every complaint? Less migtht be more here.
To use this definition, however, we need to define a diagram differently, since a diagram is a functor by definition.
In the basics of category theory, there are many different choices for what to take as fundamental definition and what as derived concept. Category theory reflects on itself in many ways.
But, yes, if we have the notion of functor given, defined in the ordinary way without reference to diagrams, then we can define
a diagram in
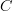 is a functor
is a functor 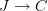
a commuting diagram is a diagram for which
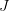 is a poset.
is a poset.
-
- CommentRowNumber157.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Since the nLab is a little easier to draw diagrams, I put some thoughts at alternative experimental definition of commutative diagram for reference.
Edit: Thanks to staring at the picture and thanks to Urs' comments, I think I get it now.
-
- CommentRowNumber158.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
@Urs: I'm just saying that at the moment, we do not have a proper definition on the nLab without using functorial langugae, so it's kinda circular.
-
- CommentRowNumber159.
- CommentAuthorEric
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
Edit: Removed a lame question I asked in a rush while headed out the door...
-
- CommentRowNumber160.
- CommentAuthorMike Shulman
- CommentTimeMar 31st 2010
- (edited Mar 31st 2010)
I think "diagram" is used with multiple meanings. Often we use it to mean, as the lab says at diagram, just a functor. But sometimes we use it to mean a map of directed graphs into the underlying graph of a category, and I think this is the sense in which we use it when we talk about whether or not a diagram commutes. (So probably diagram should be updated to reflect something like this.) And in that context, I think it is common to say that a diagram commutes if every path of parallel arrows is equal.
Note that the shape of the diagram, i.e. the domain graph of the map, matters when you ask whether a diagram commutes in this sense, even if its image in the target category consists of the same objects and arrows. If I draw a diagram
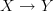 , meaning that I take the domain graph to have two vertices and one edge connecting them, then this diagram always commutes, even though the images of the two vertices may happen to be the same object to give a diagram
, meaning that I take the domain graph to have two vertices and one edge connecting them, then this diagram always commutes, even though the images of the two vertices may happen to be the same object to give a diagram 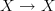 which is in fact an endomorphism. On the other hand, if I draw a diagram
which is in fact an endomorphism. On the other hand, if I draw a diagram 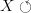 , meaning I take the domain graph to have one vertex and one edge from it to itself, then a diagram of this shape only commutes if the endomorphism is the identity.
, meaning I take the domain graph to have one vertex and one edge from it to itself, then a diagram of this shape only commutes if the endomorphism is the identity. -
- CommentRowNumber161.
- CommentAuthorMike Shulman
- CommentTimeMar 31st 2010
BTW, by adjunction, a diagram in the sense of a map
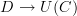 where D is a graph and C is a category and U denotes the underlying graph of a category, is the same as a functor
where D is a graph and C is a category and U denotes the underlying graph of a category, is the same as a functor 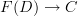 , where F denotes the free category on a graph. From this perspective, the diagram commutes iff this functor factors through the posetal quotient of
, where F denotes the free category on a graph. From this perspective, the diagram commutes iff this functor factors through the posetal quotient of 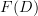 .
.I think this is the only connection with posets. In particular, I don't think it is really a good idea to talk about a diagram "commuting" or "not commuting" in the context where "diagram" means "functor."
-
- CommentRowNumber162.
- CommentAuthorUrs
- CommentTimeMar 31st 2010
I think this is the only connection with posets. In particular, I don't think it is really a good idea to talk about a diagram "commuting" or "not commuting" in the context where "diagram" means "functor."
This may be the only connection, but it is also the crucial connection. Why do you say it is not a good idea?
A commuting diagram in C is a functor from a poset to C. That looks like a good definition to me.
-
- CommentRowNumber163.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
I think perhaps Urs is thinking not of a poset, but of a category with an initial object 0 and a terminal object 1. Then the unique arrow from 0 to 1 tells us the diagram commutes. Note that not all diagrams are of this sort :)
We have a commuting loop when 0=1, I think, but check this... -
- CommentRowNumber164.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
I think "diagram" is used with multiple meanings.
Hallelujah :)
We should make this clear on the nLab.
Often we use it to mean, as the lab says at diagram, just a functor.
In this sense, a diagram must itself always be a category, right? In which case, it will always have identities even when we draw degenerate things like
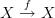 . In this case, there are actually 4 identity morphisms there. One hidden identity morphism at each vertex and two anti-parallel identity morphism spanning the vertices.
. In this case, there are actually 4 identity morphisms there. One hidden identity morphism at each vertex and two anti-parallel identity morphism spanning the vertices.If this diagram commutes, we must have
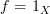 .
.But sometimes we use it to mean a map of directed graphs into the underlying graph of a category, and I think this is the sense in which we use it when we talk about whether or not a diagram commutes.
In this case, the diagram need not be a category. It is just a graph. This is the crucial point here.
In this case, there need not be identities and you do not need to fill in compositions either. The "walking square" diagram need not even have diagonals if it is just a graph.
However, I think it is usually assumed that you do "fill in composites" when talking about diagrams in the second sense even if you do not necessarily require identities.
So I propose to give this second sense of "diagram" a different name. I would call it a "semidiagram" or something or simply a "semifunctor"
Instead of saying it commutes, I might suggest "semicommutes".
The difference between these two meanings Mike highlighted basically, it seems to me, amount to different treatments of identities.
For example, you could have a loop graph semicommute and not equal the identity. In fact, this would be a good way to describe a non-trivial idempotent, i.e. an idempotent is a semicommuting loop. With a semicommuting loop, the corresponding semicommuting degenerate triangle means
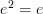 , but we do not require the loop to commute with the identity (since semidiagrams do not have identities) in which case
, but we do not require the loop to commute with the identity (since semidiagrams do not have identities) in which case 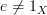 . On the other hand, a commuting loop must always equal the identity.
. On the other hand, a commuting loop must always equal the identity.If I draw a diagram
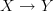 , meaning that I take the domain graph to have two vertices and one edge connecting them, then this diagram always commutes, even though the images of the two vertices may happen to be the same object to give a diagram
, meaning that I take the domain graph to have two vertices and one edge connecting them, then this diagram always commutes, even though the images of the two vertices may happen to be the same object to give a diagram 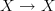 which is in fact an endomorphism. On the other hand, if I draw a diagram
which is in fact an endomorphism. On the other hand, if I draw a diagram 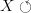 , meaning I take the domain graph to have one vertex and one edge from it to itself, then a diagram of this shape only commutes if the endomorphism is the identity.
, meaning I take the domain graph to have one vertex and one edge from it to itself, then a diagram of this shape only commutes if the endomorphism is the identity.This ambiguity only exists with semidiagrams. With a diagram (as opposed to semidiagram), a commuting degenerate arrow like that will equal the identity. With a semidiagram, a semicommuting degenerate arrow need not equal the identity and its meaning depends on the graph.
This is the crux of the disagreement between Harry and I, but it is not a disagreement about "math". It is a disagreement about what a "diagram" is. Mike highlighted two distinct meanings. I propose calling the second meaning something else, e.g. semidiagram.
-
- CommentRowNumber165.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
@ Eric
There is a difference between a diagram of shape
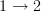 that happens to map
that happens to map 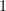 and
and 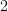 to the same object, and a diagram that has one vertex and one arrow to itself. The former is not a loop, despite picking out an endomorphism, and the latter is a loop, and it commutes if that arrow is the identity. Thus the 'image of the diagram' in the category we are considering is not enough: we need to know the shape of the diagram. When Urs draws
to the same object, and a diagram that has one vertex and one arrow to itself. The former is not a loop, despite picking out an endomorphism, and the latter is a loop, and it commutes if that arrow is the identity. Thus the 'image of the diagram' in the category we are considering is not enough: we need to know the shape of the diagram. When Urs draws 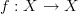 , this isn't a loop, as it has the shape of the first case above.
, this isn't a loop, as it has the shape of the first case above.With a semicommuting loop, the corresponding semicommuting degenerate triangle means
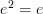
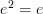 isn't described by a loop, it was a misunderstanding on Harry's part: the shape of this diagram is a triangle, and can't be anything else. It is a commuting triangle, moreover, and there is no need to introduce a new concept to describe it.
isn't described by a loop, it was a misunderstanding on Harry's part: the shape of this diagram is a triangle, and can't be anything else. It is a commuting triangle, moreover, and there is no need to introduce a new concept to describe it.Regarding non-commuting diagrams in a 1-category having imaginary 2-arrows as fillers: this isn't the case. When I said above that 2-arrows in a 1-category are equals signs, I was slightly wrong. The power of negative thinking tells us that 2-arrows are truth values, and so (assuming classical logic) we either have that it is true there is a filler (an equals sign) between two parallel 1-arrows, or it is false that there is a filler. There are no other options. The only thing you could put there is a not-equals sign, but I think this is a bit silly :) as you can't compose these (e.g.
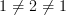 doesn't imply
doesn't imply 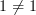 ) so they do not deserve to be called 2-arrows. The stuff that Domenico and Urs (and to a much lesser extent, I) have discussed about all connections being flat needs stuff like inner automorphism groupoids and machinery that is not particularly appropriate here, IMHO.
) so they do not deserve to be called 2-arrows. The stuff that Domenico and Urs (and to a much lesser extent, I) have discussed about all connections being flat needs stuff like inner automorphism groupoids and machinery that is not particularly appropriate here, IMHO. -
- CommentRowNumber166.
- CommentAuthorEric
- CommentTimeApr 1st 2010
When Urs draws
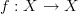 , this isn't a loop, as it has the shape of the first case above.
, this isn't a loop, as it has the shape of the first case above.Because you say it, doesn't make it so :)
What is it about the definition of diagram (which itself seems to be in dispute at the moment) tells me that
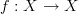 is not a loop. To me, that is simply a convenient notation for a loop. If it truly is not a loop, there should be some way to say this in a way that follows from some unambiguous definition. So far, I haven't seen that definition.
is not a loop. To me, that is simply a convenient notation for a loop. If it truly is not a loop, there should be some way to say this in a way that follows from some unambiguous definition. So far, I haven't seen that definition.Try telling a "scientist or engineer"
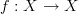 is not a loop and he/she will stare at you (kind of like I am) thinking you are a crazy :)
is not a loop and he/she will stare at you (kind of like I am) thinking you are a crazy :)I'm willing to accept it if you can show how it follows from some definition, but so far, it seems little more than a statement. I can make statements too, e.g.
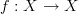 is a loop. Why is mine less correct than yours?
is a loop. Why is mine less correct than yours? -
- CommentRowNumber167.
- CommentAuthorUrs
- CommentTimeApr 1st 2010
I think perhaps Urs is thinking not of a poset, but of a category with an initial object 0 and a terminal object 1. Then the unique arrow from 0 to 1 tells us the diagram commutes.
No, poset is crucial. In a commuting diagram, every pair of parallel paths of edges is equal. That means manifestly: they are in the image of a poset.
Initial and final object are often there, but not necessarily. An infinite version of a commuting triangle diagram is a directed limit cone diagram. That has an initial object but not necessarily a terminal one.
-
- CommentRowNumber168.
- CommentAuthorUrs
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
Try telling a "scientist or engineer"
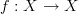 is not a loop
is not a loopI need to convince you at least, or else discussion of commuting diagrams will not progress: for a diagram, it is the vertices labeled byy objects that matter, not just the names of the objects themselves. See also Mike's comments above.
-
- CommentRowNumber169.
- CommentAuthorEric
- CommentTimeApr 1st 2010
Like I said, I can be convinced if you can show me how this follows from some definition.
As it stands, this still seems to be an axiom put it by hand. Worse, it is an unnecessary axiom that leads to confusion.
Mike's very clear comment made a lot of sense to me. As far as I can tell, neither you nor David have acknowledged the dichotomy. Does that mean you disagree with Mike?
-
- CommentRowNumber170.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
Here is a poset and commuting diagram:
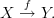
Using your definition wrt posets, here is a commuting diagram:
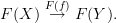
We can define
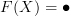
and
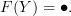
But in doing so, we have created a loop. This loop must commute, hence
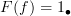 .
.Instead of a diagram, we could consider a semifunctor
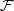 and semidiagram
and semidiagram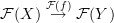 .
.We can define
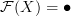
and
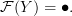
Since this loop is a semidiagram and not a diagram, it is not necessary that it commute with identities, hence in general we have
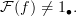
Rather than introduce a "shape dependence" (which is yucky and we should all reject on moral grounds), we can simply introduce a second notion of semidiagram. These are useful in their own right as Harry has pointed out.
Edit: I like the definition of commuting diagram in terms of posets, so I suggest:
A commuting diagram in
 is a functor from a poset
is a functor from a poset 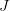 to
to  .
.A semicommuting semidiagram in
 is a semifunctor from a poset
is a semifunctor from a poset 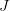 to
to  .
.Edit^2: It seems to me the choice is to retain some yucky shape dependence, OR reject shape dependence but consider semicommuting semidiagrams instead. I vote for the latter.
Edit^3: I understand why Urs might not like this because it would mean he has been working with semifunctors all along rather than functors in a lot of stuff. In other words, wherever "shape matters" in a diagram, you are actually using semifunctors and semidiagrams :)
Edit^4: Another reason to like the definition of commuting diagrams in terms of images of posets is that it is easily generalized:
A commuting
 -diagram in
-diagram in  is a functor from an
is a functor from an  -poset
-poset 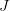 to
to  .
. -
- CommentRowNumber171.
- CommentAuthorUrs
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
Like I said, I can be convinced if you can show me how this follows from some definition.
A commuting diaagram in C is a functor from a poset to C. That's the definition that everything follows from.
But in doing so, we have created a loop. This loop must commute, hence
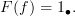
No. Stick to the definition you recalled in the sentence above this to see it: A functor from the category with a single nontrivial morphism
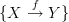 need not send that morphism to an identity morphism, not even if we assume it sends it to an endomorphism.
need not send that morphism to an identity morphism, not even if we assume it sends it to an endomorphism.It might be helpful to think of the poset generated from morphisms
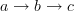 and
and 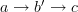 . An image of that poset in any category is a commuting square in that category, the probably most familiar kind of commuting diagram.
. An image of that poset in any category is a commuting square in that category, the probably most familiar kind of commuting diagram. -
- CommentRowNumber172.
- CommentAuthorUrs
- CommentTimeApr 1st 2010
Mike's very clear comment made a lot of sense to me. As far as I can tell, neither you nor David have acknowledged the dichotomy. Does that mean you disagree with Mike?
I dare say that we agree on something as elementary as what a commuting diagram is. If that were controversial, what business would we have here writing about category theory. That would be like disagreeing on what plus and times means.
-
- CommentRowNumber173.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
<p>Thanks Urs. I think these examples are simple enough we can pinpoint exactly where I'm confused.</p> <blockquote> <p>A functor from the category with a single nontrivial morphism <img src="/extensions/vLaTeX/cache/latex_0eb46a96d1cd1f397f0bb8efb23f0abc.png" title="\{X \stackrel{f}{\to} Y\}" style="vertical-align:-20%;" class="tex" alt="\{X \stackrel{f}{\to} Y\}" /> need not send that morphism to an identity morphism, not even if we assume it sends it to an endomorphism.</p> </blockquote> <p>Where in the definition does it say this?</p> <p>Up <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7368#Comment_7368">here</a> I explained as clearly as I am capable of explaining what I meant.</p> <p>Can we stick with this example?</p> <p>I understand that if you declare "shape matters" then what you say is true. But you do not need to declare "shape matters". You can declare "shape doesn't matter" and work with semifunctors instead. That was the whole point of my comment above (please read it!).</p> <p>I drew some pictures to help here: <a href="https://ncatlab.org/ericforgy/show/Shape+Dependence+in+Commutative+Diagrams">Shape Dependence in Commutative Diagrams (ericforgy)</a></p> -
- CommentRowNumber174.
- CommentAuthorEric
- CommentTimeApr 1st 2010
Another way to put it...
If we start with a poset
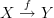
and map
 and
and  both to
both to  , we get
, we get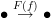
how many objects are there?
-
- CommentRowNumber175.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
<blockquote> <p>I dare say that we agree on something as elementary as what a commuting diagram is.</p> </blockquote> <p>Mike gave <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7340#Comment_7340">two meanings</a> of "diagram". Are those two meanings the same?</p> -
- CommentRowNumber176.
- CommentAuthorEric
- CommentTimeApr 1st 2010
Let me set up some statements, like bowling pins, to try to make it easy to knock one down and isolate where I'm confused.
The setup is simple. We start with a poset
 given by
given by
and a diagram
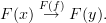
In what follows, we set
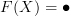
and
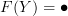
so we really have
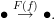
Here are the bowling pins:
 is a category since it is the image of a functor from a poset
is a category since it is the image of a functor from a poset commutes since it is the image of a poset (by definition of commute)
commutes since it is the image of a poset (by definition of commute)There is only one category with one object and one morphism
If a category with one object commutes, it has just one morphism, i.e. the identity (regardless of how we draw it)
In the category
 there is only one object
there is only one objectSince the diagram
 commutes and has just one object, it has just one morphism, i.e. the identity
commutes and has just one object, it has just one morphism, i.e. the identity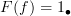
These steps seem pretty sound to me and follow your definition of commuting diagram (which I like very much by the way). At least one of them must be wrong. Which one?
Thanks
-
- CommentRowNumber177.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
The image of a category is not necessarily a category. If F(f) is not the identity then the image is not a category, as it would have to contain all the composites F(f)F(f), F(f)F(f)F(f),... which it doesn't. You cannot then use the argument that a category with one arrow has this arrow an identity. This is why I, at least, would not call
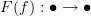 a loop unless
a loop unless 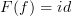 .
.A diagram which is of shape
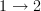 is a single arrow (or if you like there are identity arrows on the images of
is a single arrow (or if you like there are identity arrows on the images of 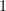 and
and 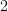 , but these make no impact). That it commutes really just says that
, but these make no impact). That it commutes really just says that 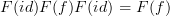 . But also that
. But also that 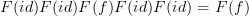 and so on. This doesn't add anything.
and so on. This doesn't add anything.A diagram is more than just its image. Maybe only in the case that all the vertices are distinct objects and the diagram is of shape a poset could you claim the image is a category. (I can't believe I didn't pick this up earlier - would have saved you some effort)
This is why the domain of the diagram is important, and even if you want to recast what a commuting diagram is, even in an informal sense, you have to absorb the nuances of the technical definition. You could have, for example, a diagram
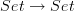 where all the objects get mapped to a single set, and all the arrows to the identity on that set, but this is certainly not the trivial diagram
where all the objects get mapped to a single set, and all the arrows to the identity on that set, but this is certainly not the trivial diagram 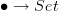 .
. -
- CommentRowNumber178.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
Thanks David.
If
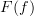 is not the identity then the image is not a category
is not the identity then the image is not a categoryThat is exactly my point. If
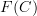 is a category, then
is a category, then 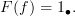
So the answer is that
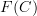 is not a category?
is not a category?How disappointing...
I believe you, but that makes me literally feel nauseous.
A more satisfying answer might have been something along the lines that there is a forgetful functor
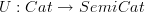
that "forgets identities". Then given categories
 and
and  , a diagram(or better "semidiagram") is a semifunctor
, a diagram(or better "semidiagram") is a semifunctor 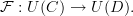
The image
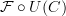
is a semicategory.
I never expected (although Harry said so) the answer was "F(C) is not a category". Ugh...
Do you see how nicely everything seems to work out if you use semicategories instead? Then you have true "shape independence". All diagrams drawn at Shape Dependence in Commutative Diagrams would be the same if interpreted as semicategories.
This "shape dependence" goes against everything I thought I ever learned about geometry and category theory.
PS: I am also very fond of the idea of defining idempotents as semicommuting loops. Since all the diagrams at Shape Dependence in Commutative Diagrams are the same as semidiagrams, then labeling the morphisms with
 instead of
instead of 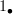 gives
gives  and
and  .
. -
- CommentRowNumber179.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
nevermind.
-
- CommentRowNumber180.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
nevermind
At one point, I said a diagram was a subcategory and you said "A diagram is not a subcategory". But within a few minutes you changed your comment to something like "Why would you want to do that?" I thought that meant you had come around and saw the error of your ways and diagrams were subcategories. My mistake.
Totally and completely unsatisfying answer. Oh well. C'est la vie.
Thanks everyone for your help. I do understand now, but I'm not happy.
-
- CommentRowNumber181.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
A functor preserves composition and identities. So where in the definition of a functor
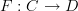 does it allow enough flexibility that
does it allow enough flexibility that 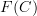 is not a subcategory of
is not a subcategory of  ?
?If
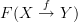 is a subcategory of
is a subcategory of  with
with 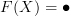 and
and 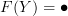 , then as David pointed out, we must have
, then as David pointed out, we must have 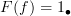 . So there must be some crack that lets us slide through so that
. So there must be some crack that lets us slide through so that 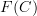 is not a category, but I don't see it.
is not a category, but I don't see it.What am I missing (besides a brain)?
Edit: I think I see. I think.
Let
 be a category with one object
be a category with one object  generated by an endomorphism
generated by an endomorphism  so that morphisms in
so that morphisms in  are of the form
are of the form 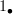 ,
,  ,
, 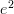 ,
, 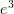 , etc.
, etc.Let
 be our favorite poset
be our favorite poset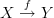
A functor
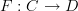 sends
sends 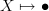 and
and 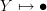 but can send
but can send 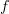 to any power of
to any power of  . It will preserve composition and it will preserve identities for any power of
. It will preserve composition and it will preserve identities for any power of  , but
, but 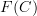 will only be a subcategory if
will only be a subcategory if 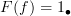 .
.Edit^2: But now, since
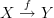 is a poset,
is a poset, 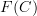 should commute in
should commute in  and I'm back to where I was before because we have one object and one morphism and it commutes, so....
and I'm back to where I was before because we have one object and one morphism and it commutes, so.... 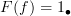 and
and 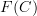 is a subcategory.
is a subcategory.I think I'm going to go jump off a building...
-
- CommentRowNumber182.
- CommentAuthorTodd_Trimble
- CommentTimeApr 1st 2010
Try this: let
 be the category with two objects
be the category with two objects  and
and 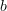 and only one non-identity morphism
and only one non-identity morphism 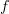 , of the form
, of the form 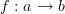 . Let
. Let  be
be 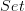 . Define a functor
. Define a functor 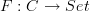 so that both
so that both 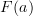 and
and 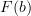 are
are 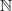 , the set of natural numbers, and
, the set of natural numbers, and 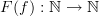 is the adding 1 (i.e., successor) function.
is the adding 1 (i.e., successor) function.The point is that the image
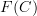 is not closed under composition, because
is not closed under composition, because 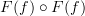 , the adding 2 function, is not in the image. So the image is not a category. (Or perhaps it would be better to say that the "naive image" -- what one thinks of the image as being ordinarily -- doesn't work.)
, the adding 2 function, is not in the image. So the image is not a category. (Or perhaps it would be better to say that the "naive image" -- what one thinks of the image as being ordinarily -- doesn't work.)Looking at this, you can see that what goes kaflooey is due to the looping behavior: you get a loop in the codomain category
 (a morphism from
(a morphism from 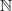 to itself) that wasn't there in the domain category
to itself) that wasn't there in the domain category  , and this looping forces one to reckon with more composites than
, and this looping forces one to reckon with more composites than  is able to "see".
is able to "see".Does this make sense?
-
- CommentRowNumber183.
- CommentAuthorEric
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
<p>Thanks Todd.</p> <p>Yes, it makes sense until my "<a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7397#Comment_7397">Edit^2</a>". According to that <img src="/extensions/vLaTeX/cache/latex_8b47ef5536afebff1b2de470b4db1b40.png" title="F(f)" style="vertical-align:-20%;" class="tex" alt="F(f)" /> should be a "commuting loop" since <img src="/extensions/vLaTeX/cache/latex_9fc3d7b3f93f91e386b477262444dd59.png" title="a\stackrel{f}{\to} b" style="vertical-align:-20%;" class="tex" alt="a\stackrel{f}{\to} b" /> is a commuting diagram and it commutes with the identity so it must be that <img src="/extensions/vLaTeX/cache/latex_a5d9bc854a2c318dc6f9e9b158eea691.png" title="F(f) = 1_\mathbb{N}" style="vertical-align:-20%;" class="tex" alt="F(f) = 1_\mathbb{N}" />.</p> <p>One thing that started me on the endless loop of mental pain was thinking that any commuting loop must be the identity.</p> <p>PS: I wouldn't expect any mortal to read this entire discussion, but <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7340#Comment_7340">here</a> is a very helpful post from Mike.</p> -
- CommentRowNumber184.
- CommentAuthorJohn Baez
- CommentTimeApr 1st 2010
Eric; you just asked me for help over at the nCafe. I can see from reading 10 or 20 of these entries that you're confused, but it's not easy to tell what you're confused by right now. So:
If you can phrase a precise and self-contained question in two or three sentences, I'll answer it. If you can't... well, in math it's important to analyze ones own confusion until one can encapsulate it in a short, sharp question.
I will say this: "diagram" is used in at least two ways in category theory: first to mean a directed graph G labelled by objects and morphisms in a category C, second to mean a functor from some other category D to the category C. It's good to be clear about the difference, but the first sort of diagram becomes the same as the second sort if we take D to be the free category on the directed graph G. -
- CommentRowNumber185.
- CommentAuthorJohn Baez
- CommentTimeApr 1st 2010
And note that if G is has one vertex and one edge (a loop), D will have infinitely many morphisms. -
- CommentRowNumber186.
- CommentAuthorEric
- CommentTimeApr 1st 2010
<p>Thanks!</p> <p>The story starts around <a href="https://ncatlab.org/nlab/show/experimental+alternative+definition+of+functor">here</a> where a fairly succinct summary is given at the top. After some twists and turns, it seems like when defining <a href="https://ncatlab.org/nlab/show/functor">functor</a> we could combine "preserves composition" and "preserves identities" into a single statement "preserves commuting diagrams" since both compositions and identities are special kinds of commuting diagrams, i.e. a commuting triangle and commuting loop respectively. I think I first wrote this on the n-Forum <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7112#Comment_7112">here</a>. Mike gave his blessing in comment #47 <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7140#Comment_7140">here</a>.</p> <p>From there, I was about to head off on a journey to see how far I could get by defining everything in terms of commuting diagrams, e.g. <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=948">Radically Elementary Category Theory</a>. Even us "scientists and engineers" can understand commuting diagrams. Or so I thought!</p> <p>Mike added another great comment along the same lines as what you just mentioned <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7340#Comment_7340">here</a> about the two meanings of "diagram". I thought I came back with a poetic response <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7356#Comment_7356">here</a>, but it landed with a thud. I thought diagrams in the first sense, i.e. functors, were categories <em>BZZT!</em> and I thought diagrams in the second sense were <a href="https://ncatlab.org/nlab/show/semicategory">semicategories</a>. I again thought I explained this in a nice way <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7368#Comment_7368">here</a>, but <em>thud</em>.</p> <p>Along the way, Urs came up with an awesome definition of commutative diagram, i.e. given a diagram <img src="/extensions/vLaTeX/cache/latex_38b1d7152754312d582c413bed6feba6.png" title="F:J\to C" style="vertical-align:-20%;" class="tex" alt="F:J\to C" />, the diagram commutes when <img src="/extensions/vLaTeX/cache/latex_fcaf008468148987ec101a472c00fc2f.png" title="J" style="vertical-align:-20%;" class="tex" alt="J" /> is a <a href="https://ncatlab.org/nlab/show/poset">poset</a>.</p> <p>In an act of desperation, I listed a bunch of statements <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7391#Comment_7391">here</a> hoping to pinpoint exactly where I go astray and it turned out to be the first step. A diagram is not necessarily a category. Argh! (Thanks David!)</p> <p>Oh my goodness, it is 2:30am and I'm about to pass out so I may need to come back to ask a decent question, but for now I will point at <a href="https://ncatlab.org/ericforgy/show/Shape+Dependence+in+Commutative+Diagrams">Shape Dependence in Commutative Diagrams (ericforgy)</a>. This whole idea of the diagrams listed there being "different" bugs me. I hope to understand that. My disheartened response is <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7394#Comment_7394">here</a>, where I cried</p> <blockquote> <p>This "shape dependence" goes against everything I thought I ever learned about geometry and category theory.</p> </blockquote> -
- CommentRowNumber187.
- CommentAuthorTodd_Trimble
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
<p>Eric, if you feel there is some conflict between my comment and your Edit^2, then I conclude there is some confusion lurking in Edit^2, or in whatever you had in mind when you wrote it. For <img src="/extensions/vLaTeX/cache/latex_8b47ef5536afebff1b2de470b4db1b40.png" title="F(f)" style="vertical-align:-20%;" class="tex" alt="F(f)" /> isn't the identity; <em>by definition</em> it's the successor function. So if you if think your Edit^2 leads you to conclude it's the identity, then clearly there's something's wrong. (To give you some credit here, I think you are confused on a slightly subtle point which I hope becomes clear.)</p> <p>(I did read that earlier comment by Mike, and I'm surprised that it didn't unconfuse you then, since you tell us now it was very helpful.)</p> <p>So: since your Edit^2 devolves around the word "commutes", it sounds to me you're probably getting confused there, i.e., by the definition of "commutative diagram". So let's go back. A <em>diagram</em> in a category <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> may be defined to be a functor <img src="/extensions/vLaTeX/cache/latex_9e0801eacdd43ef2a4b101146e67db98.png" title="F: C \to D" style="vertical-align:-20%;" class="tex" alt="F: C \to D" />, where <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a small category (called the underlying <em>scheme</em> of the diagram). Under that definition, a diagram <em>commutes</em> if, given two morphisms <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align:-20%;" class="tex" alt="f" /> and <img src="/extensions/vLaTeX/cache/latex_333d2017e7f892329a2362f4087a4bd3.png" title="g" style="vertical-align:-20%;" class="tex" alt="g" /> of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> having the same domain and having the same codomain, <img src="/extensions/vLaTeX/cache/latex_85fcb2cf89e0d4077de91402a06775cd.png" title="F(f) = F(g)" style="vertical-align:-20%;" class="tex" alt="F(f) = F(g)" />.</p> <p>In particular, any diagram whose underlying scheme is a poset is automatically commutative, because under that poset condition, given morphisms <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align:-20%;" class="tex" alt="f" /> and <img src="/extensions/vLaTeX/cache/latex_333d2017e7f892329a2362f4087a4bd3.png" title="g" style="vertical-align:-20%;" class="tex" alt="g" /> that have the same domain and have the same codomain, <img src="/extensions/vLaTeX/cache/latex_4cdc95674d8b446b2bfd8b62b530c718.png" title="f = g" style="vertical-align:-20%;" class="tex" alt="f = g" />. That was the case in my example, where I took <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to be the category given by the poset <img src="/extensions/vLaTeX/cache/latex_38d7575663ab9de678ba8a4164e0a2ce.png" title="a \leq b" style="vertical-align:-20%;" class="tex" alt="a \leq b" />.</p> <p>But let's take some other examples, since I think I see where you may be getting confused. Let's take the underlying scheme <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to be the category with just one object, and whose morphisms are in bijective correspondence with nonnegative integers, composed by adding the corresponding integers. (If you like, it's the free category generated by a directed graph which consists of just a loop. But since there seems to have been past confusion about free categories as well, I'm not sure this will help.) Then, the identity of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is represented by the integer 0 (call it <img src="/extensions/vLaTeX/cache/latex_b98a3e66c3481fb1f5c283a36e88cb1f.png" title="f_0" style="vertical-align:-20%;" class="tex" alt="f_0" />), and there is another morphism of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> represented by 1 (<img src="/extensions/vLaTeX/cache/latex_c5dde583e0df7dceec38e323070130a1.png" title="f_1" style="vertical-align:-20%;" class="tex" alt="f_1" />). These morphisms have the same domain and the same codomain, since there's only one object of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />. So now, given a commuting diagram <img src="/extensions/vLaTeX/cache/latex_9e0801eacdd43ef2a4b101146e67db98.png" title="F: C \to D" style="vertical-align:-20%;" class="tex" alt="F: C \to D" />, it follows that <img src="/extensions/vLaTeX/cache/latex_832d95584340c9f965ec7a5f606b9be8.png" title="F(f_1) = F(f_0) = F(id) = id" style="vertical-align:-20%;" class="tex" alt="F(f_1) = F(f_0) = F(id) = id" />. In fact, <img src="/extensions/vLaTeX/cache/latex_7e3cc86135b5671246f0a90ad7876b8d.png" title="F(f_n) = id" style="vertical-align:-20%;" class="tex" alt="F(f_n) = id" /> for all <img src="/extensions/vLaTeX/cache/latex_485d65c1e6e7757e4de10eb91bc9382b.png" title="n" style="vertical-align:-20%;" class="tex" alt="n" />, for the same reason. That must have been what you were thinking when you said that "commuting loops" lead inevitably to what I would the constant diagram, consisting only of the identity. Yes, but that's for this loop-scheme! Not for the scheme in my example, which has no loops!</p> <p>An example similar to the one for the preceding paragraph can be given if the scheme has just one object and just two morphisms of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />, an identity and an idempotent morphism. The conclusion again is that "commuting loops are the identity", <em>if the underlying scheme is generated by a loop</em>!</p> <p>But that conclusion doesn't hold more generally, for other schemes of different diagrams.</p> <p>So, in summary, it seems there is some confusion due to conflation of the underlying scheme <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> (which may not have any loops, as in my example) and how <img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align:-20%;" class="tex" alt="F(C)" /> appears as a subgraph of </latex>D$$. Beware of identifying diagrams with such subgraph inclusions!</p> <p>(Oh, and by the way: if Urs was defining a commutative diagram to be a functor whose underlying scheme was a poset, then I would have to disagree. If the definition is that it is diagram which as a functor which <em>factors</em> through a poset, which I think is what he and Mike agreed on somewhere but I'd have to check to make sure, then I would agree.)</p> <p>[Edit: having weird problems with Markdown. Will publish as is.]</p> -
- CommentRowNumber188.
- CommentAuthorMike Shulman
- CommentTimeApr 2nd 2010
Honestly, do you people ever do anything else besides post on this forum? (-:
The reason I would not want to apply the adjective "commuting" to a diagram-as-functor is that the word there has a different context. E.g. if I say "let
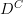 be the category of C-diagrams in D" and someone asks "do the diagrams commute or not?" I would say "you're confused---that isn't the kind of 'diagram' we're talking about here" (although hopefully I would say it more politely than that). If a diagram-as-functor commutes when it factors through (or is defined on) a poset, I would have to say "we aren't necessarily asking that they commute---but actually, you're confused, because..." I would rather have the question be a type error, hence be meaningless, than to have an answer which is irrelevant.
be the category of C-diagrams in D" and someone asks "do the diagrams commute or not?" I would say "you're confused---that isn't the kind of 'diagram' we're talking about here" (although hopefully I would say it more politely than that). If a diagram-as-functor commutes when it factors through (or is defined on) a poset, I would have to say "we aren't necessarily asking that they commute---but actually, you're confused, because..." I would rather have the question be a type error, hence be meaningless, than to have an answer which is irrelevant.In my experience, we only talk about diagrams commuting for diagrams of the sort that we actually draw on a page. And those diagrams are of the directed-graph sort, since what we draw is manifestly a directed graph. Thus I think it makes sense to restrict the usage of "commuting" to diagrams-as-graph-maps. I also think that if we were all consistently restricting it in that sense, then this whole discussion would be much less confusing. (-:
I think "semicategory" and "semifunctor" are not appropriate here, because they refer only to omitting identities, whereas in a diagram-as-graph-map there is no composition to be discussed or preserved either.
Other than that, it seems that the main point of confusion is the difference between a functor (or graph map) and its domain/image. This has already been said, but let me emphasize: a diagram is not a category, or a subcategory, or a graph, or a subgraph; a graph is a morphism from a source category or graph into a target category. If the source is a graph (as I prefer, in this context), then what the morphism does is "label" each vertex of the graph by an object of the target category, and each edge of the graph by a morphism in the target category. It seems to me that this is really what we are doing when we draw a diagram on paper: we draw a directed graph and then we label each vertex with an object and each edge with a morphism. So just as the *picture"
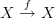 is a different picture from the picture
is a different picture from the picture  , they are two different diagrams, even though "the set of objects which label some vertex" and "the set of arrows which label some edge" are the same, respectively, in the two cases.
, they are two different diagrams, even though "the set of objects which label some vertex" and "the set of arrows which label some edge" are the same, respectively, in the two cases. -
- CommentRowNumber189.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
<p>Thanks guys!</p> <p>I owe John a question, so let me set that up first and hope it addresses some really important points you bring up.</p> <p>An example that is small enough for me to understand yet degenerate enough to illustrate the concept is the one I mentioned in the first "Edit:" <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7397#Comment_7397">here</a>, which I think is equivalent to the one Todd mentioned <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7408#Comment_7408">here</a>. It consists of a category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> given by</p> <img src="/extensions/vLaTeX/cache/latex_5574e77eb12134719f4d6ade098449fd.png" title="X\stackrel{f}{\to} Y" style="vertical-align:-20%;" class="tex" alt="X\stackrel{f}{\to} Y" /> <p>and a free category</p> <img src="/extensions/vLaTeX/cache/latex_e9a3755612281e0d8516d4cafdc1fd4e.png" title="\overset{e}{\circlearrowleft}" style="vertical-align:-20%;" class="tex" alt="\overset{e}{\circlearrowleft}" /> <p>which consists of all morphisms <img src="/extensions/vLaTeX/cache/latex_14e67d5aa5ab55d3a53ff24c0264c161.png" title="1_\bullet" style="vertical-align:-20%;" class="tex" alt="1_\bullet" />, <img src="/extensions/vLaTeX/cache/latex_9aaa2c2772d8ae53e9d59b54be9712fc.png" title="e" style="vertical-align:-20%;" class="tex" alt="e" />, <img src="/extensions/vLaTeX/cache/latex_6486aa481f56e43f2d7dfe19567672f9.png" title="e^2" style="vertical-align:-20%;" class="tex" alt="e^2" />, <img src="/extensions/vLaTeX/cache/latex_c0f8b5265f9dbe3ff316295b323d7ddb.png" title="e^3" style="vertical-align:-20%;" class="tex" alt="e^3" />, etc.</p> <p>A functor <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> sends <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align:-20%;" class="tex" alt="X" /> and <img src="/extensions/vLaTeX/cache/latex_4dc4f99626c3d159bf0a8ca65ee0e5e3.png" title="Y" style="vertical-align:-20%;" class="tex" alt="Y" /> to <img src="/extensions/vLaTeX/cache/latex_2668009033d84cdc8d16f29c11ae03fd.png" title="\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet" /> (the only place they can go) and sends <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align:-20%;" class="tex" alt="f" /> to just one morphism in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />. This is the "kaflouey" since <img src="/extensions/vLaTeX/cache/latex_5ec3dcd4fa96727f6008946ebbeebfa2.png" title="F" style="vertical-align:-20%;" class="tex" alt="F" /> can only see one morphism in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> so the only way the image of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> can be a category is if <img src="/extensions/vLaTeX/cache/latex_82b027f09c658d2b24cbab3c40e9a942.png" title="F(f) = 1_\bullet" style="vertical-align:-20%;" class="tex" alt="F(f) = 1_\bullet" />. However, even if <img src="/extensions/vLaTeX/cache/latex_91913a800e316556cac7144e92dee7fd.png" title="F(f) = e^n" style="vertical-align:-20%;" class="tex" alt="F(f) = e^n" /> for some <img src="/extensions/vLaTeX/cache/latex_a9f722090a31ec8644f7a2a0a2e22dfc.png" title="n>0" style="vertical-align:-20%;" class="tex" alt="n>0" /> it still "preserves composites" and it still "preserves identities" so it is a functor for any <img src="/extensions/vLaTeX/cache/latex_f54029c65b2b68b1cd7312dc3e7f2ccf.png" title="n\ge 0" style="vertical-align:-20%;" class="tex" alt="n\ge 0" />.</p> <p><strong>Question #1 (Warm-up):</strong> Does <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> (as above) preserve commutative diagrams?</p> <p>The answer (I think) depends on how you define commutative diagram.</p> <p>If we define "commutative diagram" in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to be a functor <img src="/extensions/vLaTeX/cache/latex_c20205ca833716468a7f197e57e1c2ee.png" title="G:J\to C" style="vertical-align:-20%;" class="tex" alt="G:J\to C" /> where <img src="/extensions/vLaTeX/cache/latex_fcaf008468148987ec101a472c00fc2f.png" title="J" style="vertical-align:-20%;" class="tex" alt="J" /> is a poset, then any poset is already a commutative diagram since we can always write <img src="/extensions/vLaTeX/cache/latex_5cc531e0ad2421775ee02cb93d99b99c.png" title="1_C:C\to C" style="vertical-align:-20%;" class="tex" alt="1_C:C\to C" /> for any poset <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />.</p> <p>This means the category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> above is a commutative diagram, so its image in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> should also be a commutative diagram.</p> <p>However, (I think) there is only one commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />, namely</p> <img src="/extensions/vLaTeX/cache/latex_2bd6bd0c73a1ba8cc15f35b89fd85a7e.png" title="\overset{1_\bullet}{\circlearrowleft}." style="vertical-align:-20%;" class="tex" alt="\overset{1_\bullet}{\circlearrowleft}." /> <p>So if <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> preserves commutative diagrams and <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a commutative diagram than <img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align:-20%;" class="tex" alt="F(C)" /> is a commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> and the only commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> is the one that sends <img src="/extensions/vLaTeX/cache/latex_5af2641454f64c181b59139543ebff15.png" title="f\mapsto 1_\bullet" style="vertical-align:-20%;" class="tex" alt="f\mapsto 1_\bullet" />.</p> <p>There seems to be a contradiction somewhere (?)</p> <p>So here it goes...</p> <blockquote> <b>Question:</b><br><br> Given categories <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> and <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> as above together with statements:<br><br> <ul> <li>A functor <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> preserves commutative diagrams</li> <li>A commutative diagram in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a functor <img src="/extensions/vLaTeX/cache/latex_c20205ca833716468a7f197e57e1c2ee.png" title="G:J\to C" style="vertical-align:-20%;" class="tex" alt="G:J\to C" /> for some poset <img src="/extensions/vLaTeX/cache/latex_fcaf008468148987ec101a472c00fc2f.png" title="J" style="vertical-align:-20%;" class="tex" alt="J" /></li> </ul><br> Does it follow that<br><br> <ul> <li><img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a poset and hence a commutative diagram</li> <li><img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align:-20%;" class="tex" alt="F(C)" /> is a commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /></li> <li>The only commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> is <img src="/extensions/vLaTeX/cache/latex_e6edc36ee79ddffa37cccd4a07678061.png" title="\overset{1_\bullet}{\circlearrowleft}" style="vertical-align:-20%;" class="tex" alt="\overset{1_\bullet}{\circlearrowleft}" /></li> <li>Since <img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align:-20%;" class="tex" alt="F(C)" /> is a commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> and the only commutative diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> is <img src="/extensions/vLaTeX/cache/latex_e6edc36ee79ddffa37cccd4a07678061.png" title="\overset{1_\bullet}{\circlearrowleft}" style="vertical-align:-20%;" class="tex" alt="\overset{1_\bullet}{\circlearrowleft}" />, then <img src="/extensions/vLaTeX/cache/latex_82b027f09c658d2b24cbab3c40e9a942.png" title="F(f) = 1_\bullet" style="vertical-align:-20%;" class="tex" alt="F(f) = 1_\bullet" /></li> </ul><br> ?<br><br> I'm guessing the last statement is false, so there must be a weak link in the chain somewhere. Where is the error? </blockquote> <p>Now you all have made statements such as</p> <blockquote> <p><a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7408#Comment_7408">Todd</a>: So, in summary, it seems there is some confusion due to conflation of the underlying scheme <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> (which may not have any loops, as in my example) and how <img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align:-20%;" class="tex" alt="F(C)" /> appears as a subgraph of <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />. Beware of identifying diagrams with such subgraph inclusions!</p> <p>[snip]</p> <p><a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7413#Comment_7413">Mike</a>: So just as the *picture" <img src="/extensions/vLaTeX/cache/latex_137a2dbe1b50eb09760cad28e6205014.png" title="X\overset{f}{\to} X" style="vertical-align:-20%;" class="tex" alt="X\overset{f}{\to} X" /> is a different picture from the picture <img src="/extensions/vLaTeX/cache/latex_e9d8b765925438490130b234aedd094d.png" title="\overset{f}{\circlearrowleft}" style="vertical-align:-20%;" class="tex" alt="\overset{f}{\circlearrowleft}" />, they are two different diagrams, even though "the set of objects which label some vertex" and "the set of arrows which label some edge" are the same, respectively, in the two cases.</p> <p>[snip]</p> <p><a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7365#Comment_7365">Eric</a>: Try telling a "scientist or engineer" <img src="/extensions/vLaTeX/cache/latex_591e591487cc49c9a6530c453c0a4014.png" title="f:X\to X" style="vertical-align:-20%;" class="tex" alt="f:X\to X" /> is not a loop</p> <p>Urs: I need to convince you at least, or else discussion of commuting diagrams will not progress: for a diagram, it is the vertices labeled byy objects that matter, not just the names of the objects themselves. See also Mike's comments above.</p> </blockquote> <p>So it could be a simple matter of me not being able to internalize (or maybe accept) that</p> <img src="/extensions/vLaTeX/cache/latex_28ff1b0538b53da70d17ee8e503afcda.png" title="\bullet\stackrel{f}{\to}\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet\stackrel{f}{\to}\bullet" /> <p>and</p> <img src="/extensions/vLaTeX/cache/latex_e9d8b765925438490130b234aedd094d.png" title="\overset{f}{\circlearrowleft}" style="vertical-align:-20%;" class="tex" alt="\overset{f}{\circlearrowleft}" /> <p>are "different" and not just different notations for the same thing. It is almost impossible for me to look at those two diagrams as anything but representing the same underlying geometrical object, i.e. a loop. How you draw it shouldn't matter.</p> -
- CommentRowNumber190.
- CommentAuthorTodd_Trimble
- CommentTimeApr 2nd 2010
Mike, I see why you think that restricting the usage in that way makes sense, and I'm happy to go along with it, but I'm not particularly fussed either way. (The imaginary dialogue you mentioned would be funny, and would take me slightly aback, but somehow it strikes me as slightly improbable. (-: ) If the restriction helps deconfuse the present discussion, then by all means let's adopt it, but I'm guessing the heart of the confusion is really the thing you pointed to at the end (and I thought injecting the word "scheme" would help shine a light on it (-:).
-
- CommentRowNumber191.
- CommentAuthorMike Shulman
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
Eric, if we consider
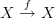 and
and 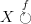 as pictures of a morphism, then they are pictures of the same thing. But they are clearly different pictures. Perhaps it will be less confusing if you think of a "diagram" as being a sort of "picture," so that we can draw two different pictures which describe the same underlying data (= "geometrical object") in the category. Certainly one and the same object can be pictured in many different ways, and we can talk about properties of one picture which may not be shared by some other picture.
as pictures of a morphism, then they are pictures of the same thing. But they are clearly different pictures. Perhaps it will be less confusing if you think of a "diagram" as being a sort of "picture," so that we can draw two different pictures which describe the same underlying data (= "geometrical object") in the category. Certainly one and the same object can be pictured in many different ways, and we can talk about properties of one picture which may not be shared by some other picture.In your example, we can draw many commutative diagrams in the category D, such as the triangle representing
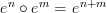 , or (the case under consideration) the single morphism
, or (the case under consideration) the single morphism 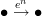 .
.@Todd, yes, I agree that my hypothetical dialogue is funny and improbable, and I don't have particularly strong feelings about my suggested usage.
-
- CommentRowNumber192.
- CommentAuthorHarry Gindi
- CommentTimeApr 2nd 2010
There is no vote for closure button on the nForum.
-
- CommentRowNumber193.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
<blockquote> <p>Mike: In your example, we can draw many commutative diagrams in the category D, such as the triangle representing <img src="/extensions/vLaTeX/cache/latex_4b3cf23233f38dc598a8310b52ff1935.png" title="e^n \circ e^m = e^{n+m}" style="vertical-align:-20%;" class="tex" alt="e^n \circ e^m = e^{n+m}" />, or (the case under consideration) the single morphism <img src="/extensions/vLaTeX/cache/latex_7da497e6be175e52a5731bde3445a348.png" title="\bullet \overset{e^n}{\to} \bullet" style="vertical-align:-20%;" class="tex" alt="\bullet \overset{e^n}{\to} \bullet" />.</p> </blockquote> <p>Yeah, that is the sticking point for me. The triangle <img src="/extensions/vLaTeX/cache/latex_4b3cf23233f38dc598a8310b52ff1935.png" title="e^n \circ e^m = e^{n+m}" style="vertical-align:-20%;" class="tex" alt="e^n \circ e^m = e^{n+m}" /> definitely semicommutes, i.e. it commutes when you "forget identities", but I'd be hesitant to say it commutes. That is why I keep <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7368#Comment_7368">talking about "semidiagrams"</a> because semidiagrams don't care about identities. But when we draw</p> <img src="/extensions/vLaTeX/cache/latex_65ce3c68bc82ed911bc6ab92ebe11913.png" title="\bullet\stackrel{e^n}{\to}\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet\stackrel{e^n}{\to}\bullet" /> <p>it automatically comes with a second (and third actually going the other way) hidden arrow</p> <img src="/extensions/vLaTeX/cache/latex_45585e0b8f6a5e899f62b6928ec93058.png" title="\bullet\underset{1_\bullet}{\stackrel{e^n}{\rightrightarrows}}\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet\underset{1_\bullet}{\stackrel{e^n}{\rightrightarrows}}\bullet" /> <p>This diagram commutes only when</p> <img src="/extensions/vLaTeX/cache/latex_4d6f1b5d789d2379ca933fb64d2b5c35.png" title="e^n = 1_\bullet." style="vertical-align:-20%;" class="tex" alt="e^n = 1_\bullet." /> <p>It doesn't matter how you draw it, a functor <img src="/extensions/vLaTeX/cache/latex_38b1d7152754312d582c413bed6feba6.png" title="F:J\to C" style="vertical-align:-20%;" class="tex" alt="F:J\to C" /> always sends <img src="/extensions/vLaTeX/cache/latex_708034a06aa448a405f48c832c13c3be.png" title="1_X" style="vertical-align:-20%;" class="tex" alt="1_X" /> to <img src="/extensions/vLaTeX/cache/latex_72ef004f6a886fd69ff9ac39d020c910.png" title="1_{F(X)}" style="vertical-align:-20%;" class="tex" alt="1_{F(X)}" /> so whether you draw one <img src="/extensions/vLaTeX/cache/latex_2668009033d84cdc8d16f29c11ae03fd.png" title="\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet" /> or two in your diagram, there is always a <img src="/extensions/vLaTeX/cache/latex_14e67d5aa5ab55d3a53ff24c0264c161.png" title="1_\bullet" style="vertical-align:-20%;" class="tex" alt="1_\bullet" /> going between them.</p> <p>Like I said, this is the sticking point.</p> <p>When the (semi)diagram is a <a href="https://ncatlab.org/nlab/show/semifunctor">semifunctor</a> <img src="/extensions/vLaTeX/cache/latex_f4e244477540d62ed965c518ff0e93fa.png" title="\mathcal{F}:J\to C" style="vertical-align:-20%;" class="tex" alt="\mathcal{F}:J\to C" />, i.e. has no identities, then we have nontrivial relations <img src="/extensions/vLaTeX/cache/latex_4b3cf23233f38dc598a8310b52ff1935.png" title="e^n \circ e^m = e^{n+m}" style="vertical-align:-20%;" class="tex" alt="e^n \circ e^m = e^{n+m}" />. This in fact gives a nice way to define idempotents, i.e. an idempotent is a semicommuting loop.</p> <p>Note added a little later: I really do appreciate all the help from everyone. I think I am close to getting this. If I can see how Mike's notion of "picture" follows from some rigorous arrow theoretic definition, then that will probably do the trick. I hope you can see that I pretty much understand these toy models well enough to talk about them and I'm kind of hung up on definitions of some of the terms. It seems there are different ways to think about diagrams. Are these all the same?</p> -
- CommentRowNumber194.
- CommentAuthorTodd_Trimble
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
<div> <p>Eric, I have a feeling that the confusion is now starting to unravel, but let's look at this:</p> <blockquote> But when we draw <img src="/extensions/vLaTeX/cache/latex_65ce3c68bc82ed911bc6ab92ebe11913.png" title="\bullet\stackrel{e^n}{\to}\bullet" style="vertical-align: -20%;" class="tex" alt="\bullet\stackrel{e^n}{\to}\bullet"/> it automatically comes with a second hidden arrow <img src="/extensions/vLaTeX/cache/latex_45585e0b8f6a5e899f62b6928ec93058.png" title="\bullet\underset{1_\bullet}{\stackrel{e^n}{\rightrightarrows}}\bullet" style="vertical-align: -20%;" class="tex" alt="\bullet\underset{1_\bullet}{\stackrel{e^n}{\rightrightarrows}}\bullet"/> </blockquote> <p>No, it doesn't! You put that in by hand!</p> <p>Think again about the <em>domain</em> category of the diagram: in your picture it has just one non-identity arrow, going between two different objects (at this point, I am now agreeing with Mike, that perhaps it would help unconfuse matters to think instead of a diagram as a graph morphism to the underlying graph of a category). That's the arrow that is labeled by a morphism in the codomain (like <img src="/extensions/vLaTeX/cache/latex_d313fabd0b0f6126cf1bc8561bd1b085.png" title="e^n" style="vertical-align: -20%;" class="tex" alt="e^n"/>) when you speak of a diagram of that shape. There is no second parallel arrow in the domain (scheme, underlying shape of the diagram, whatever you want to call it), no second arrow to be labeled by an identity or by anything else. So by sticking in that identity arrow, you've cheated: you've now changed the shape!</p> <p>Let me say it a little differently, again for this example: in the domain of the diagram, the non-identity arrow goes between <em>two different objects</em>. There is no identity arrow running between these objects in the domain, since they are different. That fact is not altered by the fact that the diagram we happen to be discussing maps them to (or labels them by) the same object in the codomain. So, there is no second parallel (identity) arrow in the domain that we are mandated to label as an identity in the codomain. Like I say, you stuck that in yourself. The domain simply doesn't have a second parallel arrow, and the rules of the game are that you label (with codomain data) only the stuff you see in the domain.</p> </div> -
- CommentRowNumber195.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
Thank you Todd! Like you said, I think I am close to getting this.
One last point...
The domain
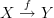
is really
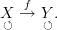
So our domain had two objects and three morphisms unless we are thinking of it as just a graph.
How many objects does the codomain have? How many morphisms does the codomain have?
The identity morphisms have to go somewhere (unless it was just a graph all along).
Also, I am confused because a diagram can apparently be a functor or it can be a morphism of graphs. Through adjunction, these two are related, but are they the same?
When you guys mention there are two ways to think about diagrams, are these two ways the same expressed differently, or are they truly different? When Mike first mentioned the two meanings, I thought they were different.
-
- CommentRowNumber196.
- CommentAuthorHarry Gindi
- CommentTimeApr 2nd 2010
This is the main consequence of the free-forgetful adjunction for categories that we took great pains to explain to you last week.
-
- CommentRowNumber197.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
<blockquote> <blockquote> <p>Eric: Also, I am confused because a diagram can apparently be a functor or it can be a morphism of graphs. Through adjunction, these two are related, but are they the same?</p> <p>When you guys mention there are two ways to think about diagrams, are these two ways the same expressed differently, or are they truly different? When <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7340#Comment_7340">Mike first mentioned the two meanings</a>, I thought they were different.</p> </blockquote> <p>Harry: This is the main consequence of the free-forgetful adjunction for categories that we took great pains to explain to you last week.</p> </blockquote> <p>So does this mean the two meanings of diagram Mike is talking about are the same? I know graph morphisms and functors are related by an adjunction so that for any graph morphism <img src="/extensions/vLaTeX/cache/latex_27cc390aec1b1c61f926a3fbe835813e.png" title="G\to U(C)" style="vertical-align:-20%;" class="tex" alt="G\to U(C)" /> there is a unique functor <img src="/extensions/vLaTeX/cache/latex_0d1483327531dd4153e5ea333e6a3753.png" title="F(G)\to C" style="vertical-align:-20%;" class="tex" alt="F(G)\to C" />. Does that mean the definition of diagram in terms of functors needs to be restricted to free categories? I didn't think so. So its not clear that <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7340#Comment_7340">Mike's two cases</a> were the same.</p> <p>Here is a statement I think I could swallow in a way that I might not worry about degenerate diagrams:</p> <blockquote> <p>Given a graph <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> and a category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />, a <strong>diagram</strong> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a graph morphism <img src="/extensions/vLaTeX/cache/latex_27cc390aec1b1c61f926a3fbe835813e.png" title="G\to U(C)" style="vertical-align:-20%;" class="tex" alt="G\to U(C)" />.</p> <p>A <strong>commutative diagram</strong> is a diagram in which <img src="/extensions/vLaTeX/cache/latex_dc743d601e5e0cf4cdd46bb2824d0b3f.png" title="F(G)" style="vertical-align:-20%;" class="tex" alt="F(G)" /> is a poset.</p> </blockquote> <p>How is that?</p> <p>Now, if I try to turn that around via adjunction, I'd say</p> <blockquote> <p>Given a graph <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> and a category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />, a <strong>diagram</strong> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a functor <img src="/extensions/vLaTeX/cache/latex_0d1483327531dd4153e5ea333e6a3753.png" title="F(G)\to C" style="vertical-align:-20%;" class="tex" alt="F(G)\to C" />.</p> <p>A <strong>commutative diagram</strong> is a diagram for which <img src="/extensions/vLaTeX/cache/latex_dc743d601e5e0cf4cdd46bb2824d0b3f.png" title="F(G)" style="vertical-align:-20%;" class="tex" alt="F(G)" /> is a poset.</p> </blockquote> <p>I've never seen diagram defined quite this way, but it seems reasonable. At least on the nLab, a diagram is just a functor <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" />.</p> <p>If this is correct, can we adopt this as the official definition?</p> -
- CommentRowNumber198.
- CommentAuthorTodd_Trimble
- CommentTimeApr 2nd 2010
<div> <blockquote> So our domain had two objects and three morphisms unless we are thinking of it as just a graph. </blockquote> <p>That's right.</p> <blockquote> How many objects does the codomain have? How many morphisms does the codomain have? </blockquote> <p>I want to say it doesn't matter -- it depends. In my original example, the codomain was <img src="/extensions/vLaTeX/cache/latex_4981dace9a12cac85b96282cad1141cb.png" title="Set" style="vertical-align: -20%;" class="tex" alt="Set"/>, so there are jillions of each. But from that large container we picked just the bit that we wanted: in the running example, we assigned $\mathbb{N}$ to both of the objects of the domain, and assigned the successor function to the non-identity arrow. We could have chosen different assignments.</p> <p>It may help to think of it this way: the domain <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/> gives you the underlying shape of the diagram, and the diagram itself is that shape together with a labeling of the parts of that shape by data which belongs to the codomain; the functor assignments give precisely that labeling.</p> <blockquote> The identity morphisms have to go somewhere (unless it was just a graph all along). </blockquote> <p>That's right: they are perforce sent to (or assigned) identity morphisms.</p> <p>I think I see where you might think this heads you toward trouble, but this is where we need very clear language to keep all the components of the picture straight and disambiguated. Assuming we are for the moment still thinking of diagrams as functors, the definition of what it means for a diagram to commute is very carefully stated: whenever <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align: -20%;" class="tex" alt="f"/> and <img src="/extensions/vLaTeX/cache/latex_333d2017e7f892329a2362f4087a4bd3.png" title="g" style="vertical-align: -20%;" class="tex" alt="g"/> are two parallel morphisms belonging to the <em>domain</em> ("parallel" meaning: have the same domain and have the same codomain), the diagram (functor) <img src="/extensions/vLaTeX/cache/latex_5ec3dcd4fa96727f6008946ebbeebfa2.png" title="F" style="vertical-align: -20%;" class="tex" alt="F"/> sends them to the same map: <img src="/extensions/vLaTeX/cache/latex_85fcb2cf89e0d4077de91402a06775cd.png" title="F(f) = F(g)" style="vertical-align: -20%;" class="tex" alt="F(f) = F(g)"/>. The diagram-picture comes in two components, really: there is the underlying scheme or shape -- that's the domain -- and then on top of that is superimposed, so to speak, a labeling of the parts of the domain by codomain data; the functor <img src="/extensions/vLaTeX/cache/latex_5ec3dcd4fa96727f6008946ebbeebfa2.png" title="F" style="vertical-align: -20%;" class="tex" alt="F"/> itself performs the labeling.</p> <p>Now: check the example against this carefully-worded definition. You'll see that the diagram commutes, no problem. As long as you keep the two aforementioned two components of the picture straight, you won't fall into paradox.</p> <blockquote> Also, I am confused because a diagram can apparently be a functor or it can be a morphism of graphs. Through adjunction, these two are related, but are they the same? </blockquote> <p>Not literally the same, no: a graph morphism <img src="/extensions/vLaTeX/cache/latex_375ac6db8532ffc69d178257a0a4cfbb.png" title="G \to U(D)" style="vertical-align: -20%;" class="tex" alt="G \to U(D)"/> into the underlying graph of a category <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align: -20%;" class="tex" alt="D"/> is not literally, or in terms of strict logic, the same as a functor <img src="/extensions/vLaTeX/cache/latex_cadb5f19893654cd2fa1ccb665e136a0.png" title="F(G) \to D" style="vertical-align: -20%;" class="tex" alt="F(G) \to D"/> from the free category on a graph <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align: -20%;" class="tex" alt="G"/>. But you can go back and forth freely, and these notions carry essentially the same information.</p> <blockquote> When you guys mention there are two ways to think about diagrams, are these two ways the same expressed differently, or are they truly different? When Mike first mentioned the two meanings, I thought they were different. </blockquote> <p>That's right -- they are different. But spiritually speaking, not different in any very significant sense. To be precise, the meaning of diagram I was using, where we use any category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/> as domain and <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/>-diagrams in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align: -20%;" class="tex" alt="D"/> are functors <img src="/extensions/vLaTeX/cache/latex_b8084f37bc2b84e2ef0a212ed3bc8bd3.png" title="C \to D" style="vertical-align: -20%;" class="tex" alt="C \to D"/>, is strictly more general than Mike's meaning (where we use graph morphisms <img src="/extensions/vLaTeX/cache/latex_375ac6db8532ffc69d178257a0a4cfbb.png" title="G \to U(D)" style="vertical-align: -20%;" class="tex" alt="G \to U(D)"/>, or equivalently functors <img src="/extensions/vLaTeX/cache/latex_cadb5f19893654cd2fa1ccb665e136a0.png" title="F(G) \to D" style="vertical-align: -20%;" class="tex" alt="F(G) \to D"/> coming out of free categories). But Mike was arguing that in actual practice, we just about always use the meaning he gave, and the one I gave has extra somewhat spurious generality not needed in practice. I believe I agree with that, and neither of us seem to be too exercised about the distinction.</p> <p>@Harry: please don't speak down to Eric. He is trying, and I believe I am correct in saying that while he knows a lot of mathematics, he is an engineer by training, and is coming from a different scientific culture. I think we all agree that mathematics is hard, and we need to be patient toward those who are struggling and have the courage to expose that fact. (You may not be a professional teacher now, but you are probably contemplating such a track, and it's never too soon to train oneself to become a helping teacher.)</p> </div> -
- CommentRowNumber199.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
<p>Thanks again Todd! Quick note...</p> <p>When I said "same", I didn't mean "literally the same", I should have said something like "Was it an adjunction that <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7340#Comment_7340">Mike was talking about here</a>? Was he simply expressing the same concept in different contexts implicitly using an adjunction? Or were the differences more than that?"</p> <p>I think you just answered in the affirmative. Mike was implicitly using the adjunction (although he explicitly mentioned it in his next comment). Right?</p> -
- CommentRowNumber200.
- CommentAuthorTodd_Trimble
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
<div> <p>I think my last comment addressed some of your questions, except for where you tender this suggestion:</p> <blockquote> A commutative diagram is a diagram in which F(G) is a poset. </blockquote> <p>I'm glad you brought that up. I wouldn't agree with it though, because it rules out the possibility of having any loops in <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align: -20%;" class="tex" alt="G"/>.</p> <p>It <em>would</em> be correct to say, however, that a diagram <img src="/extensions/vLaTeX/cache/latex_57692eca3f93f29b3582d21504dcd5f8.png" title="Free(G) \to D" style="vertical-align: -20%;" class="tex" alt="Free(G) \to D"/> commutes if it factors through a poset (or preorder): can be expressed as a composite functor <img src="/extensions/vLaTeX/cache/latex_c7e7213bca879361643e07fc87a2ae89.png" title="Free(G) \to P \to D" style="vertical-align: -20%;" class="tex" alt="Free(G) \to P \to D"/> where <img src="/extensions/vLaTeX/cache/latex_0827b2155898e7e29e51b4330f4c0e75.png" title="P" style="vertical-align: -20%;" class="tex" alt="P"/> is a preorder. That's a sort of slick and tricky way to restate the condition I mentioned earlier: that whenever <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align: -20%;" class="tex" alt="f"/> and <img src="/extensions/vLaTeX/cache/latex_333d2017e7f892329a2362f4087a4bd3.png" title="g" style="vertical-align: -20%;" class="tex" alt="g"/> are parallel morphisms of <img src="/extensions/vLaTeX/cache/latex_bfcfae52c824f60bfd5e0a2b0950e6fa.png" title="Free(G)" style="vertical-align: -20%;" class="tex" alt="Free(G)"/> (i.e., paths in <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align: -20%;" class="tex" alt="G"/> which start at the same place and end at the same place), that <img src="/extensions/vLaTeX/cache/latex_85fcb2cf89e0d4077de91402a06775cd.png" title="F(f) = F(g)" style="vertical-align: -20%;" class="tex" alt="F(f) = F(g)"/>. There are other ways of putting it too.</p> <p>Edit: Eric #49 -- that's right.</p> </div>