nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeDec 22nd 2009
motivated by the blog discussion I added to rational homotopy theory a section Differential forms on topological spaces
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeDec 22nd 2009
- (edited Dec 22nd 2009)
I see that there was an entry by Tim Porter, that I had forgotten about: differential forms on simplices. I put a link to that in the context at rational homotopy theory now.
I also edited that entry a bit: the first paragraph said that this is to be the first entry in a sequence of three, but as far as I can see Tim has since not followed up on this. So I removed his announcement (saved it at the bottom of the entry, actually). Also, I see that the entry doesn't actually say anything about polynomial forms so far...
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeDec 22nd 2009
- (edited Dec 22nd 2009)
I am wondering about the following:
there is a Quillen adjunction
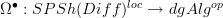 that sends an oo-stack on the cat of manifolds to its deRham algebra.
that sends an oo-stack on the cat of manifolds to its deRham algebra.Moreover, there is a theorem that says that the left Bousfield localization
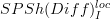 of
of 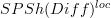 at all the cylinder projections
at all the cylinder projections 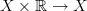 is Quillen equivalent to
is Quillen equivalent to 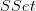 .
.Let
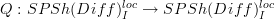 be cofibrant replacement in this localized structure. Then we get the composite functor
be cofibrant replacement in this localized structure. Then we get the composite functor 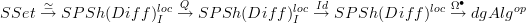 .
.Looking at what this does on objects, it seems it should be related to the Sullivan-forms functor
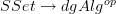 . Has anyone thought about this or seen other people think about it?
. Has anyone thought about this or seen other people think about it? -
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeDec 28th 2009
- (edited Dec 28th 2009)
I am a little confused about "diff forms on top spaces". The equivalence of cat of simplicial sets and of topological spaces is just as infty topoi, isn't it ? I mean the construction in Sullivan's word is eventually a construction in PL-world and for a topologists the world of say topological manifolds and the world of PL-manifolds is nontrivially different (and some people done a lot on documenting this difference) and this is not repaired by the infty machinery. What do you think ?
Another thing which could be of interest to discuss here is the business of D-modules. Namely the semialgebraic triangulations of semialgebraic sets play role in the theory of constructible sheaves and dualities in the theory of D-modules involving them. Regarding that this is also a non-smooth setup for generalizations of connections, there might be some common points in the theory. But here positive characteristics works also fine.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeApr 21st 2010
I expanded the section on Sullivan models.
Probably eventually this should be split off into a separate entry.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeApr 21st 2010
Ah, no!! I accidentally erased it all…
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeApr 21st 2010
Phew. I got it back out of my browser’s cache. Luckily, that remembers all the content of the edit panes in the nLab edit pages.
Anyway, the new content that I put in is now at Sullivan model.
-
- CommentRowNumber8.
- CommentAuthorjim_stasheff
- CommentTimeJan 12th 2013
The paper on Deformations of Rational Homotopy Types
arXiv:1211.1647
that Mike and I posted has received only one substantial comment.
We'd like to submit it for pub but with any improvements suggested. -
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeJan 12th 2013
- (edited Jan 12th 2013)
That’s Mike Schlessinger. (By typing [Deformations of Rational Homotopy Types](http://arxiv.org/abs/1211.1647), you get a clickable link: Deformations of Rational Homotopy Types, provided that you choose a format which supports Markdown. I usually use Markdown+Itex.)
-
- CommentRowNumber10.
- CommentAuthorjim_stasheff
- CommentTimeJan 13th 2013
Thanks, Todd - I'm still somewhat illiterate, though not a luddite. -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJan 14th 2016
- (edited Jan 14th 2016)
I have edited a little bit at rational homotopy theory (that whole entry needs a serious polishing and completion at some point):
gave the rationalization adjunction in the Sullivan approach its own subsection, such as to make it easier to spot this key statement in the entry;
expanded just a little there, but this deserves to be expanded further;
started an Examples-section with the example of rational spheres.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 14th 2016
- (edited Jan 14th 2016)
And I have merged the section previously titled “Lie-theoretic models” into the Idea-section, for it just surveys the models that are then described in the following sections. Re-edited a little in the process.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 14th 2016
Ah, I see that the example of rational -spheres was also requested at Sullivan model and at rational topological space. Therefore I now gave it its own dedicated entry and linked to from there:
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeFeb 15th 2017
- (edited Feb 15th 2017)
I would like to bring the entry rational homotopy theory into better shape. Today I have been expanding and streamlining the section on the Sullivan approach.
-
- CommentRowNumber15.
- CommentAuthorDavidRoberts
- CommentTimeOct 30th 2017
Added the reference FelixHalperin
Yves Félix and Steve Halperin, Rational homotopy theory via Sullivan models: a survey, arXiv:1708.05245
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeApr 12th 2018
added pointer to Buijs-Murillo 12 (dg-models for non-connected rational spaces)
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeJan 5th 2019
- (edited Jan 5th 2019)
added full publication data for
- Kathryn Hess, Rational homotopy theory: a brief introduction, contribution to Summer School on Interactions between Homotopy Theory and Algebra, University of Chicago, July 26-August 6, 2004, Chicago (arXiv:math.AT/0604626), chapter in Luchezar LAvramov, Dan Christensen, William Dwyer, Michael Mandell, Brooke Shipley (eds.), Interactions between Homotopy Theory and Algebra, Contemporary Mathematics 436, AMS 2007 (doi:10.1090/conm/436)
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeAug 19th 2020
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeAug 23rd 2020
added publication data for
- Yves Félix, Steve Halperin, Rational homotopy theory via Sullivan models: a survey, Notices of the International Congress of Chinese Mathematicians Volume 5 (2017) Number 2 (arXiv:1708.05245, doi:10.4310/ICCM.2017.v5.n2.a3)
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeAug 23rd 2020
added pointer to:
- Yves Félix, John Oprea, Daniel Tanré, Algebraic models in geometry, Oxford University Press 2008 (pdf, ISBN:9780199206520)
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeSep 3rd 2020
- (edited Sep 3rd 2020)
added these pointers on generalizing RHT to arbitrary fundamental groups:
Antonio Gómez-Tato, Stephen Halperin, Daniel Tanré, Rational Homotopy Theory for Non-Simply Connected Spaces, Transactions of the American Mathematical Society, Transactions of the American Mathematical Society Vol. 352, No. 4 (Apr., 2000), pp. 1493-1525 (33 pages) (jstor:118074)
Syunji Moriya, Rational homotopy theory and differential graded category, Journal of Pure and Applied Algebra, Volume 214, Issue 4, April 2010, Pages 422-439 (doi:10.1016/j.jpaa.2009.06.015)
Urtzi Buijs, Yves Félix, Aniceto Murillo, Daniel Tanré, Homotopy theory of complete Lie algebras and Lie models of simplicial sets, Journal of Topology (2018) 799-825 (arXiv:1601.05331, doi:10.1112/topo.12073)
-
- CommentRowNumber22.
- CommentAuthornLab edit announcer
- CommentTimeJun 17th 2022
-
- CommentRowNumber23.
- CommentAuthornLab edit announcer
- CommentTimeJul 22nd 2023
-
- CommentRowNumber24.
- CommentAuthornLab edit announcer
- CommentTimeJul 22nd 2023
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeMay 8th 2024
added pointer to:
- Urtzi Buijs, Yves Félix, Aniceto Murillo, Daniel Tanré, Lie Models in Topology, Progress in Mathematics 335, Springer (2020) [doi:10.1007/978-3-030-54430-0]
-
- CommentRowNumber26.
- CommentAuthornLab edit announcer
- CommentTimeNov 12th 2024
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeNov 12th 2024
Thanks. Just a propos, let me highlight that this references is also already cited at Borel-equivariant rational homotopy theory.
1 to 27 of 27