Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: rational homotopy theory

Bottom of Page

1 to 27 of 27

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeDec 22nd 2009
    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeDec 22nd 2009
    • (edited Dec 22nd 2009)

    I see that there was an entry by Tim Porter, that I had forgotten about: differential forms on simplices. I put a link to that in the context at rational homotopy theory now.

    I also edited that entry a bit: the first paragraph said that this is to be the first entry in a sequence of three, but as far as I can see Tim has since not followed up on this. So I removed his announcement (saved it at the bottom of the entry, actually). Also, I see that the entry doesn't actually say anything about polynomial forms so far...

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeDec 22nd 2009
    • (edited Dec 22nd 2009)

    I am wondering about the following:

    there is a Quillen adjunction 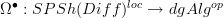\Omega^\bullet : SPSh(Diff)^{loc} \to dgAlg^{op} that sends an oo-stack on the cat of manifolds to its deRham algebra.

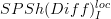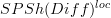    Moreover, there is a theorem that says that the left Bousfield localization SPSh(Diff)_{I}^{loc} of SPSh(Diff)^{loc} at all the cylinder projections 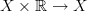X \times \mathbb{R} \to X is Quillen equivalent to SSet .

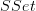    Let 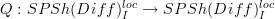Q : SPSh(Diff)_I^{loc} \to SPSh(Diff)_I^{loc} be cofibrant replacement in this localized structure. Then we get the composite functor SSet \stackrel{\simeq}{\to} SPSh(Diff)_I^{loc} \stackrel{Q}{\to} SPSh(Diff)_I^{loc} \stackrel{Id}{\to} SPSh(Diff)^{loc} \stackrel{\Omega^\bullet}{\to} dgAlg^{op} .

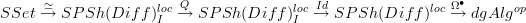    Looking at what this does on objects, it seems it should be related to the Sullivan-forms functor 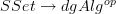SSet \to dgAlg^{op} . Has anyone thought about this or seen other people think about it?

    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeDec 28th 2009
    • (edited Dec 28th 2009)

    I am a little confused about "diff forms on top spaces". The equivalence of cat of simplicial sets and of topological spaces is just as infty topoi, isn't it ? I mean the construction in Sullivan's word is eventually a construction in PL-world and for a topologists the world of say topological manifolds and the world of PL-manifolds is nontrivially different (and some people done a lot on documenting this difference) and this is not repaired by the infty machinery. What do you think ?

    Another thing which could be of interest to discuss here is the business of D-modules. Namely the semialgebraic triangulations of semialgebraic sets play role in the theory of constructible sheaves and dualities in the theory of D-modules involving them. Regarding that this is also a non-smooth setup for generalizations of connections, there might be some common points in the theory. But here positive characteristics works also fine.

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeApr 21st 2010

    I expanded the section on Sullivan models.

    Probably eventually this should be split off into a separate entry.

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeApr 21st 2010

    Ah, no!! I accidentally erased it all…

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeApr 21st 2010

    Phew. I got it back out of my browser’s cache. Luckily, that remembers all the content of the edit panes in the nLab edit pages.

    Anyway, the new content that I put in is now at Sullivan model.

    • CommentRowNumber8.
    • CommentAuthorjim_stasheff
    • CommentTimeJan 12th 2013
    The paper on Deformations of Rational Homotopy Types
    arXiv:1211.1647
    that Mike and I posted has received only one substantial comment.
    We'd like to submit it for pub but with any improvements suggested.
    • CommentRowNumber9.
    • CommentAuthorTodd_Trimble
    • CommentTimeJan 12th 2013
    • (edited Jan 12th 2013)

    That’s Mike Schlessinger. (By typing [Deformations of Rational Homotopy Types](http://arxiv.org/abs/1211.1647), you get a clickable link: Deformations of Rational Homotopy Types, provided that you choose a format which supports Markdown. I usually use Markdown+Itex.)

    • CommentRowNumber10.
    • CommentAuthorjim_stasheff
    • CommentTimeJan 13th 2013
    Thanks, Todd - I'm still somewhat illiterate, though not a luddite.
    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeJan 14th 2016
    • (edited Jan 14th 2016)

    I have edited a little bit at rational homotopy theory (that whole entry needs a serious polishing and completion at some point):

    • gave the rationalization adjunction in the Sullivan approach its own subsection, such as to make it easier to spot this key statement in the entry;

    • expanded just a little there, but this deserves to be expanded further;

    • started an Examples-section with the example of rational spheres.

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeJan 14th 2016
    • (edited Jan 14th 2016)

    And I have merged the section previously titled “Lie-theoretic models” into the Idea-section, for it just surveys the models that are then described in the following sections. Re-edited a little in the process.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeJan 14th 2016

    Ah, I see that the example of rational nn-spheres was also requested at Sullivan model and at rational topological space. Therefore I now gave it its own dedicated entry and linked to from there:

    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeFeb 15th 2017
    • (edited Feb 15th 2017)

    I would like to bring the entry rational homotopy theory into better shape. Today I have been expanding and streamlining the section on the Sullivan approach.

    • CommentRowNumber15.
    • CommentAuthorDavidRoberts
    • CommentTimeOct 30th 2017

    Added the reference FelixHalperin

    Yves Félix and Steve Halperin, Rational homotopy theory via Sullivan models: a survey, arXiv:1708.05245

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeApr 12th 2018

    added pointer to Buijs-Murillo 12 (dg-models for non-connected rational spaces)

    diff, v81, current

    • CommentRowNumber17.
    • CommentAuthorUrs
    • CommentTimeJan 5th 2019
    • (edited Jan 5th 2019)

    added full publication data for

    diff, v87, current

    • CommentRowNumber18.
    • CommentAuthorUrs
    • CommentTimeAug 19th 2020

    added pointer to

    diff, v103, current

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeAug 23rd 2020

    added publication data for

    diff, v106, current

    • CommentRowNumber20.
    • CommentAuthorUrs
    • CommentTimeAug 23rd 2020

    added pointer to:

    diff, v106, current

    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeSep 3rd 2020
    • (edited Sep 3rd 2020)

    added these pointers on generalizing RHT to arbitrary fundamental groups:

    diff, v109, current

  22. added a brief paragraph about doing rational homotopy theory in homotopy type theory

    Anonymous

    diff, v121, current

  23. Correction to the citation of Serre’s article.

    Paul Le Meur

    diff, v125, current

  24. Another correction on the same title -which i had missed before i checked my 1st edit.

    Paul Le Meur

    diff, v125, current

    • CommentRowNumber25.
    • CommentAuthorUrs
    • CommentTimeMay 8th 2024

    added pointer to:

    diff, v133, current

  26. Added a reference to a discussion about degenerations of rationalization functors for all spaces.

    https://link.springer.com/article/10.1007/s10114-022-2063-9

    Sergei O. Ivanov

    diff, v135, current

    • CommentRowNumber27.
    • CommentAuthorUrs
    • CommentTimeNov 12th 2024

    Thanks. Just a propos, let me highlight that this references is also already cited at Borel-equivariant rational homotopy theory.

1 to 27 of 27

  1.