Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes

Show all

9061 to 9120 of 14422

  1. <
  2. 1
  3. ...
  4. 148
  5. 149
  6. 150
  7. 151
  8. 152
  9. 153
  10. 154
  11. 155
  12. ...
  13. 241
  14. >

    • Page created, but author did not leave any comments.

      v1, current

    • Page created, but author did not leave any comments.

      Anonymous

      v1, current

    • splitting this off from AdS3/CFT2 as an entry just listing references, to be !includeed into the References-lists of other entries

      v1, current

    • starting a category:reference-entry – not done yet (on my phone here…)

      v1, current

    • (created my own page because I have a huge ego)

      v1, current

    • starting something – not done yet but need to save

      v1, current

    • Detection of the 21cm hydrogen absorption line expected in the CMB has been claimed now. Such a detection is thought to have implications for observational cosmology comparable in relevance to those of the recent gravitational wave detection. I have collected some original articles and reviews here in an otherwise empty entry hydrogen line

    • Fixed link to Leonardo Rastelli, Lectures on open/closed string duality

      Anonymous

      diff, v3, current

    • stub entry, for the moment just so as to satisfy links

      v1, current

    • I keep having the need to point to something like mass gap problem. So now I created a stub for it, just so that the links works. Has to be expanded, clearly.

    • created just to satisfy liunks, but I added a minimum of an Idea-section

      v1, current

    • stub, for the moment just so as to satisfy links

      v1, current

    • added a graphics showing length scales of fundamental physics in the observable universe

      diff, v4, current

    • Todd points out elsewhere that there is a problem with the following sentence in the section Smallness in the context of universes:

      CC is essentially UU-small if there is a bijection from its set of morphisms to an element of UU (the same for the set of objects follows); this condition is non-evil.

      (introduced in revision 11).

      It looks to me that first of all this is not the right condition – the right condition must mention equivalence of categories to a U-small category.

      diff, v31, current

    • I came to think that the term geometric type theory for the type theory internal toi sheaf toposes should exists. Thanks to Bas Spitter for pointing out that Steve Vickers had already had the same idea (now linked to at the above entry).

      Also created geometric homotopy type theory in this vein, with some evident comments.

    • This is a base topic of my contribution. It introduces a new function that gives series whose coefficients are powers of fine structure constant. Furthermore each member represents natural physical interaction. It can be treated as natural physics that introduces natural particles.

      May be I made a lot of mistakes. I will correct them.

      v1, current

    • added a further quote from

      interview with Mike Duff by Graham Fermelo, The universe speaks in numbers – Interview 14 (web):

      (7:04) The problem we face is that we have a patchwork understanding of M-theory, like a quilt. We understand this corner and that corner, but what’s lacking is the overarching big picture. So directly or indirectly, my research hopes to explain what M-theory really is. We don’t know what it is.

      In a certain sense, and this is not a popular statement, I think it’s premature to be asking: “What are the empirical consequences”, because it’s not yet in a mature enough state, where we can sensibly make falsifiable prediction.

      diff, v13, current

    • a stub, for the moment just for completeness and to satisfy links

      v1, current

    • Page created, but author did not leave any comments.

      v1, current

    • I have completed the writeup of the proof of the cartesian closure of categories of presheaves: now this prop. (the argument that the evident formula for the internal hom really works had been missing)

      diff, v18, current

    • added some words to proton decay. In particular I recorded the recent claims that there is a mechanism for realistic GUTs to avoid proton decay entirely, after all:

      • Andreas Mütter, Michael Ratz, Patrick K.S. Vaudrevange, Grand Unification without Proton Decay (arXiv:1606.02303)

      • Bartosz Fornal, Benjamin Grinstein, SU(5)SU(5) Unification without Proton Decay, Physics Review Letters (arXiv:1706.08535)

      Added a similar remark to GUT in a new section Relation to proton decay.

    • Added a couple of pages where his name appears.

      diff, v2, current

    • Added section on Cluster spaces, which generalize Convergence spaces.

      Anonymous

      diff, v29, current

    • Page created, but author did not leave any comments.

      Viet

      v1, current

    • created Theta category (made disk category a redirect).

      In the "Idea" section I had the idea that the quickest way to define 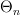\Theta_n is as the full subcategory of strict n-catgeories on n-computads. Is that right? If not, something along these lines must be right.

    • brief category: people-entry for hyperlinking references at homology of iterated loop spaces

      (many more references to Dyer on the nnLab are waiting to be hyperlinked by the energetic algebraic topologists contributing here…)

      v1, current

    • starting something – not done yet

      v1, current

    • brief category:people-entry for hyperlinking references

      v1, current

    • starting something, in order to record Theorem 4.2 in

      But HELP: The article states this without proof. I understand how the discussion here and in the other articles now cited in the entry goes towards the proof, but I’d really like to see the actual proof written out. Eventually.

      v1, current

    • Page created, but author did not leave any comments.

      Viet

      v1, current

    • Page created, but author did not leave any comments.

      v1, current

    • The article symmetric simplicial set claims that "symmetric set" is also used in the literature.

      The green box alludes to a paper by Fiedorowicz and Loday as a source for this terminology.
      However, the term "symmetric set" is nowhere to be found in this paper.

      A search on MathSciNet reveals zero matches for "symmetric set" in this sense.

      It seems to me that the name "symmetric set" is nLab's invention
      and is not actually used in the literature.

      I suggest that the article be renamed to "symmetric simplicial set".

9061 to 9120 of 14422

  1. <
  2. 1
  3. ...
  4. 148
  5. 149
  6. 150
  7. 151
  8. 152
  9. 153
  10. 154
  11. 155
  12. ...
  13. 241
  14. >
Top of Page