nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
- Discussion Type
- discussion topicLie algebroid theory
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by zskoda
- Last Active Apr 10th 2010
in reply to discussion on the blog I
added more details to Lie algebroid
added a reference by Courant to Lie algebroid, Poisson Lie algebroid and tangent Lie algebroid
created Legendre transformation as a placeholder that currently just serves to keep some references on Legendre transformation from the point of view of Lie algebroid theory.
- Discussion Type
- discussion topicautonomous double categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Apr 10th 2010
I have started to work out a slew of definitions at autonomous double category. Work in progress.
- Discussion Type
- discussion topicobservable
- Category Latest Changes
- Started by zskoda
- Comments 8
- Last comment by Tim_van_Beek
- Last Active Apr 9th 2010
New entry observable wanted at many entries. For now the very basic stuff, with a view toward maximal generality.
- Discussion Type
- discussion topicsoliton
- Category Latest Changes
- Started by zskoda
- Comments 3
- Last comment by zskoda
- Last Active Apr 9th 2010
- Discussion Type
- discussion topicThesis finished!
- Category Latest Changes
- Started by Guest
- Comments 16
- Last comment by Tim_Porter
- Last Active Apr 9th 2010
- I have put a copy of my thesis, as it is being handed up for examination, on my personal web.
David Roberts
- Discussion Type
- discussion topicunbiased composites in double categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 6
- Last comment by Eric
- Last Active Apr 8th 2010
Added some comments about the possibility of 2-dimensional unbiased composites in double categories.
- Discussion Type
- discussion topiccoinductive Trimble oo-categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 26
- Last comment by DavidRoberts
- Last Active Apr 8th 2010
I added some comments to Trimble n-category regarding a coinductive way to state the definition, which I think is very clean and neat, and also a little mind-blowing.
- Discussion Type
- discussion topicIan: latest changes
- Category Latest Changes
- Started by Ian_Durham
- Comments 10
- Last comment by Andrew Stacey
- Last Active Apr 7th 2010
- As per someone's suggestion, I am going to do what Zoran does and have one, continuously running forum topic with my latest changes.
My latest change: added response to Zoran's query at quantum mechanics.
- Discussion Type
- discussion topiccontributors to algebraic geometry
- Category Latest Changes
- Started by zskoda
- Comments 4
- Last comment by zskoda
- Last Active Apr 7th 2010
While Prof. Joyal in his joyalscatlab keeps the lists of contributors to category theory and to homological algebra, I thought it might be useful to have some complementary list for 2-3 other fields in our nlab. But this could be too much work. So I restrained with contributors to algebraic geometry, as over 20 are alerady present in the nlab anyway (algebraic geometry has much being intertwined with the development of category theory since Serre and Grothendieck). Created Jean-Pierre Serre and Shigeru Mukai, wanted also at the Timeline entry; and David Mumford. This entry should be useful as we do not have top entry of contents for alegbraic geometry. (and I do not plan it soon).
- Discussion Type
- discussion topicDonaldson-Thomas invariant
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Apr 7th 2010
Idea at Donaldson-Thomas invariant, hopefully correct to zeroth approximation, but not sure. Related update of Dominic Joyce.
- Discussion Type
- discussion topicquasi-category theory contents
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 7th 2010
created floating toc quasi-category theory contents
there is still a lot left to type in concerning quasi-category theory, but it seemed to me about time to collect what is there and organize it, so that one can see what we have, what is missing, and so that readers find their way to their information
- Discussion Type
- discussion topicspam at factorization algebra
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Eric
- Last Active Apr 7th 2010
some Anonymous Coward added an unmotivated link to some web-hosting site at factorization algebra. I have rolled back the entry to before that edit.
I am wondering if the creatures who do such things wiill at least eventually learn something from reading about things like factorization algebras...
- Discussion Type
- discussion topicgeneralized multicategories
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Apr 6th 2010
I have been greatly expanding the entry generalized multicategory, to work up gradually from the most explicit and easy-to-understand Leinster definition through profunctors, double categories, and up to the most general situation considered in my paper with Geoff, with examples. There's lots more left to do, but I have to run to a seminar now.
- Discussion Type
- discussion topicGrothendieck's existence theorem
- Category Latest Changes
- Started by zskoda
- Comments 1
- Last comment by zskoda
- Last Active Apr 6th 2010
New entry Grothendieck existence along with many redirects. New person entry Steven Kleiman. Pdf link to write up of Gerd Faltings' 1995 Bonn lectures at moduli space of bundles and some new reference here and there.
- Discussion Type
- discussion topicDold fibrations
- Category Latest Changes
- Started by DavidRoberts
- Comments 1
- Last comment by DavidRoberts
- Last Active Apr 6th 2010
I fixed up an obvious error in a claim at Dold fibration: the counterexample there showed the converse of what was claimed (and I think the error was due to me). Now I'd like to find a proper counterexample, so I'll ask on MathOverflow, in case anyone has one up their sleeve.
- Discussion Type
- discussion topichom-object in a quasi-category
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 5th 2010
created hom-object in a quasi-category
- Discussion Type
- discussion topicGrothendieck fibration
- Category Latest Changes
- Started by Mike Shulman
- Comments 5
- Last comment by Tim_Porter
- Last Active Apr 5th 2010
Did some reorganizing at Grothendieck fibration.
- Discussion Type
- discussion topicSVG Editor HowTo
- Category Latest Changes
- Started by Andrew Stacey
- Comments 12
- Last comment by Andrew Stacey
- Last Active Apr 4th 2010
Created SVG Editor HowTo whilst trying to convert the codecogs monstrosity at exercise in groupoidification - the path integral to SVG (conversion happening in the Sandbox for the moment, and definitely not finished yet).
- Discussion Type
- discussion topicA partial addition and some added details
- Category Latest Changes
- Started by Ian_Durham
- Comments 3
- Last comment by Ian_Durham
- Last Active Apr 3rd 2010
- I began working on a page for the GNS construction but started dozing off at my keyboard (so it needs someone to help finish it). Also I added a note on QBism and category theory to the page on quantum states. In it I assert that category theory is, in essence, a theory about relations (bear with me on this one - read the entry).
- Discussion Type
- discussion topicquantum state
- Category Latest Changes
- Started by Ian_Durham
- Comments 12
- Last comment by Ian_Durham
- Last Active Apr 3rd 2010
- Added page quantum state.
- Discussion Type
- discussion topic‘folk’
- Category Latest Changes
- Started by TobyBartels
- Comments 4
- Last comment by Mike Shulman
- Last Active Apr 2nd 2010
I added a brief note to folk model structure to reflect the other terms suggested on another thread.
- Discussion Type
- discussion topicmonoidal bicategories
- Category Latest Changes
- Started by Mike Shulman
- Comments 4
- Last comment by Mike Shulman
- Last Active Apr 2nd 2010
Started monoidal bicategory with a bunch of references to the tortuous literature on braided and symmetric things. Please correct me if I left anything out. It would be nice to have the "accepted/correct" definitions here eventually, for reference.
- Discussion Type
- discussion topicSome updates
- Category Latest Changes
- Started by Ian_Durham
- Comments 7
- Last comment by Ian_Durham
- Last Active Apr 2nd 2010
- Didn't have much free time, but managed to add a little bit to Stokes phenomenon and responded to Zoran's query about Birkhoff's theorem. I suggested we rename it "Birkhoff-von Neumann theorem" so as not to confuse it with other similarly titled theorems.
- Discussion Type
- discussion topicGroup Presentation
- Category Latest Changes
- Started by Tim_Porter
- Comments 2
- Last comment by zskoda
- Last Active Apr 1st 2010
I have started an entry on group presentations. This will lead to a discussion of identities among relations as well as feeding into the rewriting page.
- Discussion Type
- discussion topicNew page: [[proper subset]]
- Category Latest Changes
- Started by TobyBartels
- Comments 41
- Last comment by Mike Shulman
- Last Active Mar 31st 2010
Not much there, but I created it: proper subset.
- Discussion Type
- discussion topicClassical field theory
- Category Latest Changes
- Started by Ian_Durham
- Comments 3
- Last comment by Ian_Durham
- Last Active Mar 29th 2010
- I added a query to classical field theory.
- Discussion Type
- discussion topic"Graphical" quantum channels
- Category Latest Changes
- Started by Ian_Durham
- Comments 9
- Last comment by Eric
- Last Active Mar 29th 2010
- I broke out a very rough page on what I'm tentatively calling graphical quantum channels. If anyone has some time or interest, it's really rough and I could use some help further developing this. Essentially, my aim is to develop a fully robust theory of quantum channels in category theoretic terms, but with an eye for pedagogy and simplicity.
- Discussion Type
- discussion topicmultisymplectic geometry
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by zskoda
- Last Active Mar 29th 2010
created multisymplectic geometry by effectively reproducing a useful survey website (see references given). But added a few wrapping sentences on the nLab perspective
- Discussion Type
- discussion topicMenagerie
- Category Latest Changes
- Started by Tim_Porter
- Comments 3
- Last comment by Tim_Porter
- Last Active Mar 27th 2010
I have given a list of chapters and section headings for the Menagerie notes (first 10 chapter).
- Discussion Type
- discussion topicpartially ordered dagger category
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Mar 27th 2010
there have been recent edits at partially ordered dagger category. i edited a bit in an attempt to polish.
Tim Porter mentions parially ordered groupoids here. I am not sure why. These are not dagger categories, are they? This should go in another entry then, I suppose?
- Discussion Type
- discussion topiccartesian morphism
- Category Latest Changes
- Started by Urs
- Comments 5
- Last comment by Urs
- Last Active Mar 26th 2010
added to cartesian morphism
in the section for ordinary categories the definition in terms of pullbacks of over-categories
in the section on (oo,1)-categories more details on the definition and a very useful equivalent reformulation
- Discussion Type
- discussion topicregular singular point
- Category Latest Changes
- Started by zskoda
- Comments 1
- Last comment by zskoda
- Last Active Mar 25th 2010
The basic notion (though in fact nontrivial) regular singular point needed at Fuchsian equation. Redirects irregular singular point.
- Discussion Type
- discussion topicKapranov's NCG
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Mar 25th 2010
New entries Kapranov's noncommutative geometry and Dmitry Kaledin. New references and typographic improvements at noncommutative algebraic geometry.
- Discussion Type
- discussion topicFuchsian equation
- Category Latest Changes
- Started by zskoda
- Comments 3
- Last comment by zskoda
- Last Active Mar 25th 2010
- Discussion Type
- discussion topictype theory -- help!
- Category Latest Changes
- Started by Urs
- Comments 35
- Last comment by Urs
- Last Active Mar 25th 2010
I have to admit that I simply cannot parse many of the entries on type theory and related.
Now, this is certainly my fault, as I am not spending any considerable time to follow this. But on the other hand my impression is that many statements here are not overly complicated, and that I ought to be following at least roughly what's going on. But I don't.
One thing is that when I try to look up precise definitions such as at type theory I run into long pieces of text. I am not sure what to make of this.
My understanding was at some point that all of type theory is really just another way of speaking about categories. Instead of "object"
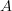 we say "type"
we say "type"  . Instead of morphism
. Instead of morphism 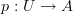 we say
we say 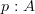 "
"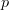 is of type
is of type  " and the like.
" and the like.Can we have some Rosetta-stone entry where all the type-theoretic language is translated into plain category theory this way?
For instance I am suspecting that what is going on at identity type is somehow another way of saying equalizer. But I am not sure. Can anyone help me?
- Discussion Type
- discussion topicgeometrical optics
- Category Latest Changes
- Started by zskoda
- Comments 6
- Last comment by zskoda
- Last Active Mar 24th 2010
I wrote a stub geometrical optics with redirect geometric optics (maybe it was better other way around, I don't have the feeling which is more used). And created stub optics. Geometric optics is of course in my present program of semiclassical approximation, equivariant localization, wall crossing, (edit typo:) Stokes phenomenon and related notions. Note that in physicscontents we still do have it listed but not written entry deformation quantization. So I just starting a stub.
- Discussion Type
- discussion topicslope filtration
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Mar 24th 2010
- Discussion Type
- discussion topicequivalence in a quasi-category
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 24th 2010
created stub for equivalence in a quasi-category. Just because i needed to link to something.
- Discussion Type
- discussion topicFundamental Bigroupoids and 2-Covering Spaces
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Mar 24th 2010
created reference-entry on David Roberts' thesis:
and linked to it from Whitehead tower in an (infinity,1)-topos
(David, I slightly edited your nLab-page, accordingly)
- Discussion Type
- discussion topicWhitehead tower in an (oo,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 23rd 2010
<p>motivated by Domenico's <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=905&page=1#Item_40">latest comment</a> I copied the material on Whitehead towers in (oo,1)-toposes from the end of <a href="https://ncatlab.org/nlab/show/universal+covering+space">universal covering space</a> into a dedicated entry:</p> <ul> <li><a href="https://ncatlab.org/nlab/show/Whitehead+tower+in+an+%28infinity%2C1%29-topos">Whitehead tower in an (infinity,1)-topos</a></li> </ul>
- Discussion Type
- discussion topicExtremal quantum channels & open systems
- Category Latest Changes
- Started by Ian_Durham
- Comments 2
- Last comment by Urs
- Last Active Mar 23rd 2010
- Since the original quantum channel entry was getting long, I broke out open quantum systems into its own page and added a page for extremal quantum channels. Both could greatly benefit from some category-theoretic input.
- Discussion Type
- discussion topicholonomic D-module
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Mar 22nd 2010
A bit of additions to holonomic D-module, a new reference at D-module and new stub characteristic variety.
- Discussion Type
- discussion topicMarkov chains, part deux
- Category Latest Changes
- Started by Ian_Durham
- Comments 2
- Last comment by Eric
- Last Active Mar 22nd 2010
- I posted a quick query on Markov chains.
- Discussion Type
- discussion topicTalk on categorical quantum channels
- Category Latest Changes
- Started by Ian_Durham
- Comments 1
- Last comment by Ian_Durham
- Last Active Mar 22nd 2010
- Due to popular demand (well, maybe not) I have uploaded my presentation to the APS March Meeting from Friday. It can be found here. I linked it from the bottom of the quantum channel page.
- Discussion Type
- discussion topicquantum mechanics in terms of †-compact categories
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Ian_Durham
- Last Active Mar 21st 2010
started stub for quantum mechanics in terms of dagger-compact categories
this is going to have some overlap with the material that is or is planned at quantum information, but I thought it would be worthwhile to have a page explicitly dedicated to the description using technology from dagger-compact categories.
- Discussion Type
- discussion topicEntanglement
- Category Latest Changes
- Started by Ian_Durham
- Comments 1
- Last comment by Ian_Durham
- Last Active Mar 20th 2010
- Based on a discussion I had with someone after my talk today, I tossed an idea up on the entanglement page concerning how to use categories to model the process of entangling something which I think could be extremely useful to physicists. But it needs a bit of work and I have a plane to catch. I will note that the idea came to me during the conversation when I recalled p. 36 in Steve Awodey's book.
- Discussion Type
- discussion topicAQFTpolishe
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Eric
- Last Active Mar 20th 2010
polished and expanded the Idea-section at AQFT
- Discussion Type
- discussion topicDurov, Skoda et al
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by zskoda
- Last Active Mar 19th 2010
Zoran,
concerning your paper with Durov and the sheaf category defined on p. 22, I am wondering:
it would almost seem as if something essentially equivalent is obtained if we would very slightly change the definition of the site (Rings with a chosen nilpotent ideal) and think of it as the tangent category of the category of rings, i.e. of Mod, thought of as being the category of square-0-extensions of rings.
So I am suggesting that we look at sheaves on (the opposite of) Mod
Do you see what I mean?
- Discussion Type
- discussion topiccochains on simplicial sets
- Category Latest Changes
- Started by zskoda
- Comments 5
- Last comment by Urs
- Last Active Mar 17th 2010
Why the pluralized title in cochains on simplicial sets, unlike in the rest of nlab ? In addition the second plural "on simplicial sets" is misleading, as if it we were talking about cochains defined on a collection of simplicial sets, rather than cochains on a single simplicial set.
Typoi discussoin, collectoin...
- Discussion Type
- discussion topicsmooth structure of path groupoid
- Category Latest Changes
- Started by Andrew Stacey
- Comments 3
- Last comment by Andrew Stacey
- Last Active Mar 17th 2010
Started smooth structure of the path groupoid in response to Theo Something-Or-Other's question on MO. Initial input concerns the structure of the path groupoid in Euclidean space with a - perhaps surprising - conclusion.
- Discussion Type
- discussion topicUniversal Homotopy Theories
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 16th 2010
created a reference-entry on Dugger's article Universal Homotopy Theories
- Discussion Type
- discussion topicglobal model structure on simplicial presheaves
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 16th 2010
polished/expanded the Idea-section at global model structure on simplicial presheaves
- Discussion Type
- discussion topicCech model structure on sheaves
- Category Latest Changes
- Started by Mike Shulman
- Comments 3
- Last comment by Urs
- Last Active Mar 16th 2010
I have a couple of questions at Cech model structure on simplicial presheaves.
- Discussion Type
- discussion topic(oo,1)-category of (oo,1)-functors
- Category Latest Changes
- Started by Urs
- Comments 5
- Last comment by Mike Shulman
- Last Active Mar 16th 2010
expanded (infinity,1)-category of (infinity,1)-functors : more details, more statements, more proofs. In particular concerning the model by the global model structure on functors.
- Discussion Type
- discussion topicspin structure as quantum anomaly cancellation
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Mar 15th 2010
added the original references that discuss how a spin strucvture on a space is the quantum anomaly cancellation condition for the superparticle sigma-model to spin structure
- Discussion Type
- discussion topicind-scheme
- Category Latest Changes
- Started by zskoda
- Comments 3
- Last comment by zskoda
- Last Active Mar 15th 2010
I have created an entry ind-scheme. This is a slightly wider topic than formal scheme, hence it deserves a separate entry, at least to record interesting references. Kapranov and Vasserot wrote a series of 4 articles in which they studied loop schemes, in a setup wider than those classifying loops in affine schemes (passage from affine to nonaffine situation is very nontrivial here, as the loops do not need to be localized so there is no descent property reducing it to loops in affine case), and an interesting result is the factorization monoid structure which is eventually responsible for factorization algebras in CFT. This should be compared to the approach via derived geometry a la Lurie and Ben-Zvi where topological loop spaces are used to obtain a similar structure.
- Discussion Type
- discussion topicReedy categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 21
- Last comment by Eric
- Last Active Mar 15th 2010
Created direct category and generalized Reedy category (well, un-stubbified the latter) as spinoffs from Reedy category.
- Discussion Type
- discussion topicfibration sequence
- Category Latest Changes
- Started by domenico_fiorenza
- Comments 4
- Last comment by domenico_fiorenza
- Last Active Mar 12th 2010
- in fibration sequence, changed the second diagram after "But the hom-functor has the crucial property..."
please someone check with the previos version to see if my correction is correct.
- Discussion Type
- discussion topicoo-groupoid
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 11th 2010
expanded the entry infinity-groupoid
- Discussion Type
- discussion topicomega-nerve
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 11th 2010
expanded omega-nerve
added to Kan complex a section on how to think of them as oo-groupoids.