nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
- Discussion Type
- discussion topiccohomology
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by zskoda
- Last Active Nov 20th 2009
wrote a fairly long Idea section at cohomology
since the question keeps coming up and I noticed that the entry did a rather suboptimal job of describing the nice observation to be described here.
- Discussion Type
- discussion topicQuery at [[2-pullback]]
- Category Latest Changes
- Started by TobyBartels
- Comments 12
- Last comment by zskoda
- Last Active Nov 20th 2009
Zoran has already reported a query at 2-pullback, but I think that it should have wider exposure. I attempted a response.
- Discussion Type
- discussion topicFull iamge
- Category Latest Changes
- Started by Guest
- Comments 1
- Last comment by Guest
- Last Active Nov 20th 2009
- Discussion Type
- discussion topicTwo new articles
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Nov 20th 2009
- dual equivalence, pretty stubby, to take links that don't like they really want to go to either duality or opposite category
- full image, not so stubby
- Discussion Type
- discussion topicnegative thinking
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 19th 2009
added to negative thinking an explicit list of related entries and the floating higher cat theory toc
I think this is important enough to show the reader as much of the grand picture as possible
- Discussion Type
- discussion topicNew article: TAC
- Category Latest Changes
- Started by TobyBartels
- Comments 3
- Last comment by Urs
- Last Active Nov 19th 2009
I figured that we could stand to have an article on TAC, so I started one.
- Discussion Type
- discussion topicGelfand-Neumark
- Category Latest Changes
- Started by David_Corfield
- Comments 14
- Last comment by zskoda
- Last Active Nov 19th 2009
- I thought I'd add something about the Gelfand-Neumark theorem
The category of commutative von Neumann algebras is contravariantly equivalent to the category of localizable measurable spaces.
to measurable space, but see we don't have anything on localizability.
I also mentioned the theorem at von Neumann algebra. But what should one then say that a general von Neumann algebra is a noncommutative localizable measurable space? Normally one says noncommutative measure space.
- Discussion Type
- discussion topicRequest for references at commutative algebraic theory
- Category Latest Changes
- Started by Andrew Stacey
- Comments 4
- Last comment by Andrew Stacey
- Last Active Nov 18th 2009
The stuff at commutative algebraic theory is very interesting and I'd like to know some references! *looks at Todd, Toby, and Gavin*
- Discussion Type
- discussion topicDanger Todd Trimble!
- Category Latest Changes
- Started by TobyBartels
- Comments 2
- Last comment by Todd_Trimble
- Last Active Nov 18th 2009
I may have overlapped an edit with you at initial algebra. ( It's no longer locked, but you didn't change it again, so maybe it timed out.)
- Discussion Type
- discussion topicmodel structure on simplicial presheaves and related
- Category Latest Changes
- Started by Urs
- Comments 13
- Last comment by Mike Shulman
- Last Active Nov 18th 2009
Over on MO Denis-Charles Cisinki kindly replied to some issues that I am recently working on here. See this.
- Discussion Type
- discussion topicCograph
- Category Latest Changes
- Started by Eric
- Comments 45
- Last comment by Eric
- Last Active Nov 17th 2009
It's not technically part of the main nLab (yet), but I asked a question at
- Discussion Type
- discussion topicdouble nerve
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Nov 17th 2009
created stub entry for double nerve in reply to this MO question.
- Discussion Type
- discussion topicmodel structure on homotopical presheaves
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 17th 2009
started model structure on homotopical presheaves, where I collect the information that Denis-Charles Cisinski kindly provided here
I created a section "higher oo-stacks" at infinity-stack with a sentence about and a link to that.
- Discussion Type
- discussion topicn-symplectic manifold
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by Urs
- Last Active Nov 17th 2009
created n-symplectic manifold
- Discussion Type
- discussion topicionads
- Category Latest Changes
- Started by Guest
- Comments 1
- Last comment by Guest
- Last Active Nov 17th 2009
- Couple of points (pun not intended) at ionad. Also remark about categorified subobject classifiers
David Roberts
- Discussion Type
- discussion topicRearranged higher category theory contents
- Category Latest Changes
- Started by TobyBartels
- Comments 5
- Last comment by TobyBartels
- Last Active Nov 17th 2009
I rearranged higher category theory - contents. It seemed wrong to have everything as a special case of
 -categories/
-categories/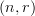 -categories except for
-categories except for  -categories/
-categories/ -categories. But it seemed right to list the latter up front, as the all-subsuming concept. So I basically reversed the order. (I also added a few entries.)
-categories. But it seemed right to list the latter up front, as the all-subsuming concept. So I basically reversed the order. (I also added a few entries.)
- Discussion Type
- discussion topicLambek's theorem; natural numbers
- Category Latest Changes
- Started by Todd_Trimble
- Comments 1
- Last comment by Todd_Trimble
- Last Active Nov 16th 2009
- Added to initial algebra the proof of Lambek's theorem, that the algebra structure of an initial algebra is an isomorphism. Also added to natural numbers object Freyd's finite colimit characterization in a topos, with a partial proof of same.
- Discussion Type
- discussion topicThe remains of JA
- Category Latest Changes
- Started by TobyBartels
- Comments 3
- Last comment by Mike Shulman
- Last Active Nov 16th 2009
We now have several new (or not so new) logic stubs: boolean domain, boolean function, boolean-valued function, higher-order logic, Peirce's law, propositional logic, ternary relation, type, Charles Sanders Peirce.
- Discussion Type
- discussion topicLevi-Civita connection
- Category Latest Changes
- Started by amathew
- Comments 2
- Last comment by Urs
- Last Active Nov 16th 2009
I created Levi-Civita connection.
- Discussion Type
- discussion topicdiagrammatic order
- Category Latest Changes
- Started by Mike Shulman
- Comments 5
- Last comment by Mike Shulman
- Last Active Nov 16th 2009
Created diagrammatic order. I attempted to strike a neutral tone in describing the dispute, but if you think I failed, please help.
- Discussion Type
- discussion topicGeneralised smooth algebras
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Nov 13th 2009
I fixed some formatting and put up some boxes at generalized smooth algebra.
- Discussion Type
- discussion topicDold fibration
- Category Latest Changes
- Started by Guest
- Comments 9
- Last comment by Urs
- Last Active Nov 13th 2009
- Created Dold fibration
- Discussion Type
- discussion topicsuspension object
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 13th 2009
quick stub for suspension object
- Discussion Type
- discussion topicfibration of bigroupoids
- Category Latest Changes
- Started by Guest
- Comments 1
- Last comment by Guest
- Last Active Nov 13th 2009
- created fibration of bigroupoids - will gather soon there some relevant background and try to define what I feel is a topologically inspired version, springing from the brief discussion at Grothendieck fibration.
David Roberts
- Discussion Type
- discussion topicKlein-2-geometry links
- Category Latest Changes
- Started by Guest
- Comments 2
- Last comment by David_Corfield
- Last Active Nov 12th 2009
- I've notices that the links at Klein 2-geometry to the earlier parts are broken (something to do with the pages at Geocities). I recall hearing that someone made some more permanent copies. Is this true and if so, where are they?
I said some embarrassingly naive things there, but one must preserve what progress was made.
-David Roberts
- Discussion Type
- discussion topicE-k-operad
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by Mike Shulman
- Last Active Nov 12th 2009
created stub for E-k-operad
- Discussion Type
- discussion topiccochains on simplicial sets
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Eric
- Last Active Nov 11th 2009
created cochains on simplicial sets
I reference there a very useful but unpublished note by Peter May that he sent me by email after he got over his astonishment that I didn't know that the Eilenberg-Zilber E_oo operad acts on cochains on a simplicial set.
It would be great if I were allowed to upload this note to the nLab and link it at that entry. I'll see if I ask by email, but maybe Mike can mention it over lunch? I feel like Peter May feels already pestered enough by my ignorance.
- Discussion Type
- discussion topiccategorification
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Nov 11th 2009
I expanded categorification a little.
I had intended to point to it from a MathOverflow question, but now I feel the entry is still too underdeveloped. Hopefully we'll eventually find the time and energy to enter the big examples that drive the interest in categorification.
- Discussion Type
- discussion topicEilenberg-Zilber operad
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 11th 2009
created Eilenberg-Zilber operad
- Discussion Type
- discussion topicdirectory of personal webs
- Category Latest Changes
- Started by Andrew Stacey
- Comments 6
- Last comment by Eric
- Last Active Nov 11th 2009
- Discussion Type
- discussion topicbraided monoidal 2-categories
- Category Latest Changes
- Started by bwebster
- Comments 2
- Last comment by Urs
- Last Active Nov 10th 2009
I started a page on braided monoidal 2-category. Not that I have anything interesting to say on the subject, but I would like to know how to get them as module 2-categories over a monoidal category.
- Discussion Type
- discussion topicthin homotopy
- Category Latest Changes
- Started by Guest
- Comments 2
- Last comment by Urs
- Last Active Nov 10th 2009
created thin homotopy to service bicategory, at which I added the necessary qualifier 'Hausdorff' to the existence of the quotient of Pi_2 by thin homotopies. There is only a passing mention of the smooth version as I only needed the topological case.
-David Roberts
- Discussion Type
- discussion topicanafunctors between fibres of a Grothendieck fibration
- Category Latest Changes
- Started by Guest
- Comments 1
- Last comment by Guest
- Last Active Nov 9th 2009
- At cartesian morphism a query/request for an anafunctor treatment of what is essentially the pseudofunctor associated to a fibration
David Roberts
- Discussion Type
- discussion topicSandbox
- Category Latest Changes
- Started by Andrew Stacey
- Comments 4
- Last comment by Andrew Stacey
- Last Active Nov 9th 2009
Actually, taking a look at the Sandbox, it's a bit full up and could do with a clean out (I shan't comment on what one usually finds in sandboxes in children's playgrounds ...). I propose we copy any serious words of wisdom to the HowTo, blank the Sandbox, and replace with a link to its own history.
I know, I know, it's a wiki so I ought to just do it, but I figured that this was something I should get some consensus on first to see if it's just me that doesn't like it.
- Discussion Type
- discussion topicdouble category
- Category Latest Changes
- Started by Mike Shulman
- Comments 2
- Last comment by Urs
- Last Active Nov 6th 2009
Added some more text and examples to double category, and moved one reference to n-fold category.
- Discussion Type
- discussion topicunit enriched category
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Nov 4th 2009
Created unit enriched category.
- Discussion Type
- discussion topiccogroup
- Category Latest Changes
- Started by David_Corfield
- Comments 14
- Last comment by Urs
- Last Active Nov 3rd 2009
- Discussion Type
- discussion topicderived group scheme and derived elliptic curve
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 3rd 2009
- created derived group scheme and derived elliptic curve
- Discussion Type
- discussion topicYoneda lemma for (oo,1)-categories
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 3rd 2009
- briefly created Yoneda lemma for (infinity,1)-categories
- Discussion Type
- discussion topicclassical limit
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Nov 3rd 2009
- started classical limit
- Discussion Type
- discussion topicCourant-Dorfman algebra
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 3rd 2009
- created Courant-Dorfman algebra (with just a brief idea and a reference so far)
- Discussion Type
- discussion topicChristoffel symbol
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Nov 3rd 2009
- created Christoffel symbol for the MathOverflow discussion at http://mathoverflow.net/questions/3847/what-is-the-geometric-significance-of-cartans-structure-equations
- Discussion Type
- discussion topicCovariant derivative
- Category Latest Changes
- Started by amathew
- Comments 1
- Last comment by amathew
- Last Active Nov 2nd 2009
Created covariant derivative.
- Discussion Type
- discussion topic[[ordered pair]]
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Nov 2nd 2009
I started ordered pair to discuss how one might define such a thing in various foundations of mathematics.
- Discussion Type
- discussion topiccategorified gram-schmidt
- Category Latest Changes
- Started by Todd_Trimble
- Comments 1
- Last comment by Todd_Trimble
- Last Active Nov 1st 2009
I added a section to Gram-Schmidt process on "categorified Gram-Schmidt" (which would apply to 2-Hilbert spaces). This is illustrated with some representation-theoretic calculations which James Dolan showed me years ago; even though the write-up is still in a raw state, the calculations are way cool and should not be lost to posterity.
- Discussion Type
- discussion topicQuestions for Mike (or whoever) …
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Oct 31st 2009
… at regular category and skeleton.
- Discussion Type
- discussion topicHow do we weaken the Horn filling condition to get simplicial (?,0)-categories?
- Category Latest Changes
- Started by StephenGaito
- Comments 2
- Last comment by Urs
- Last Active Oct 31st 2009
I have just posed the question:
If we want to weaken this even further to provide a simplicial model of, for example, a ((?,2)-category?, how would we do this? Would we apply the lifting condition on all but three of the indicies… and if so which three? (The first, last and ????)at quasi-category.
Any and all thoughts would be appreciated.
- Discussion Type
- discussion topicsuper q-Schur algebra
- Category Latest Changes
- Started by bwebster
- Comments 5
- Last comment by Urs
- Last Active Oct 30th 2009
I added an entry on super q-Schur algebras in hopes of luring people over from a MathOverflow question.
- Discussion Type
- discussion topicRiemannian metric
- Category Latest Changes
- Started by amathew
- Comments 2
- Last comment by Urs
- Last Active Oct 30th 2009
I created a page for Riemannian metric based on a "blog post": http://deltaepsilons.wordpress.com/2009/10/27/riemannian-metrics-and-connections/ and a suggestion of Urs Schreiber.
- Discussion Type
- discussion topicloopy
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by Guest
- Last Active Oct 30th 2009
I added an "idea" to loop space . Not claiming, though, that everybody will find this idea the most helpful one. But to some extent I think it is.
I had another look at delooping
Eric, you drew some nice-looking diagrams there in the discussion section. At some point in the discussion I say that I don't understand these diagram. I still don't! :-)
It would be nice if we could converge on this, because then we could move the diagrams out of the discussion into the text as a useful illustration.
Could you describe in words what you mean these diagrams are depicting? I am guessing that probably we are just thinking of what an arrow and a point means in such a diagram differently. Let's sort this out. If we agree that the diagrams make sense they should feature more prominently, if we come to the conclusion that there is some misunderstanding we should put a clearer warning to the reader.
- Discussion Type
- discussion topicassociated idempotent monad
- Category Latest Changes
- Started by Todd_Trimble
- Comments 1
- Last comment by Todd_Trimble
- Last Active Oct 29th 2009
I added a section to idempotent monad on the idempotent monad associated with a monad.
- Discussion Type
- discussion topicis passage to the CE-algebra a Quillen adjunction?
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Oct 29th 2009
I have been polishing the entry Chevalley-Eilenberg algebra on my personal web a bit.
I thought it would be good to announce here what it is that I am currently thinking about. If nothing else, this will explain which entries you all see me working on here and thereby maybe facilitate interaction more.
So currently I am thinking about the sought-for proposition that is now stated in the section Properties at the above entry. It sure looks like something like this proposition ought to be right, but I am not there yet.
- Discussion Type
- discussion topicHamiltonian mechanics
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by zskoda
- Last Active Oct 28th 2009
I thought of it and then moved the material on Hamiltonian mechanics from symplectic geometry to its own entry at Hamiltonian mechanics
- Discussion Type
- discussion topicSchur functors
- Category Latest Changes
- Started by TobyBartels
- Comments 10
- Last comment by bwebster
- Last Active Oct 28th 2009
Todd started Schur functor. I added internal links and wrote linear category to be the target of one of them.
- Discussion Type
- discussion topicnew reference: Bott, Shulman, Stasheff
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by David_Corfield
- Last Active Oct 28th 2009
added the classical article by Bott-Shulman-Stasheff to the list of references at simplicial deRham complex
- Discussion Type
- discussion topicnew references: Goerss and Lurie
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Oct 28th 2009
I was kindly being alerted that the following long-awaited references are now available:
Paul Goerss's account of the Hopkins-Miller-Lurie theorem, now linked to at A Survey of Elliptic Cohomology
Lurie part VI on little cubes oo-operads, now linked to from Jacob Lurie
- Discussion Type
- discussion topicCompletion
- Category Latest Changes
- Started by David_Corfield
- Comments 17
- Last comment by David_Corfield
- Last Active Oct 28th 2009
- Rather than ask whether it's worth it and have Urs say "do it, don't talk about it!", I started a page to compare different notions of completion. Fortunately, we are well supplied with experts on the subject. What would be great would be a comparison of different completion processes. How widely they are applicable, e.g., to the enriched case? In which situations two or more coincide, etc.
- Discussion Type
- discussion topicStrict epimorphism
- Category Latest Changes
- Started by Guest
- Comments 2
- Last comment by Mike Shulman
- Last Active Oct 28th 2009
- A question at strict epimorphism for Mike Shulman. Or anyone else who has thought about bicategorical notions of epimorphisms.
-David Roberts
- Discussion Type
- discussion topicn-categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Oct 28th 2009
Started a list at n-category of all the existing definitions of higher categories and comparisons between them. I'm sure I'm missing some, so please help!
- Discussion Type
- discussion topichigher order proposition
- Category Latest Changes
- Started by JonAwbrey
- Comments 5
- Last comment by JonAwbrey
- Last Active Oct 28th 2009
Opened a page at higher order proposition.