nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
- Discussion Type
- discussion topicidempotent adjunction
- Category Latest Changes
- Started by Mike Shulman
- Comments 9
- Last comment by zskoda
- Last Active Feb 1st 2010
Created idempotent adjunction. Does anyone know a published reference for this notion?
- Discussion Type
- discussion topicDirected joins
- Category Latest Changes
- Started by TobyBartels
- Comments 2
- Last comment by TobyBartels
- Last Active Feb 1st 2010
A little article: directed join
- Discussion Type
- discussion topicultrafilters
- Category Latest Changes
- Started by David_Corfield
- Comments 1
- Last comment by David_Corfield
- Last Active Feb 1st 2010
- Found some exposition by Todd on the web to add to ultrafilter, and a quote by Michal Barr added at ultraproduct.
This was prompted by a comment by Terry Tao
>There are two main facts that makes ultralimit analysis powerful. The first is that one can take ultralimits of arbitrary sequences of objects, as opposed to more traditional tools such as metric completions, which only allow one to take limits of Cauchy sequences of objects.
So are ultralimits in his sense a form of completion?
- Discussion Type
- discussion topicquestions on structured (infty,1)-topoi
- Category Latest Changes
- Started by Mike Shulman
- Comments 57
- Last comment by Urs
- Last Active Feb 1st 2010
Several naive questions at structured (infinity,1)-topos.
- Discussion Type
- discussion topicOpen maps
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Jan 31st 2010
Definitions for topological spaces, locales, and toposes here: open map.
- Discussion Type
- discussion topicNew article: CABAs
- Category Latest Changes
- Started by TobyBartels
- Comments 6
- Last comment by TobyBartels
- Last Active Jan 31st 2010
Does anybody know of a definition of CABA (which would not literally be complete atomic Boolean algebra) such that the theorem that the CABAs are (up to isomorphism of posets) precisely the power sets is constructively valid?
If you do, you can put it here: CABA.
- Discussion Type
- discussion topicPreservation of limits
- Category Latest Changes
- Started by TobyBartels
- Comments 3
- Last comment by TobyBartels
- Last Active Jan 31st 2010
I created a page on this topic: preserved limit. (We also need reflected limit and created limit.)
I'm not sure about the stuff at the bottom.
- Discussion Type
- discussion topiccohomology
- Category Latest Changes
- Started by Urs
- Comments 13
- Last comment by Mike Shulman
- Last Active Jan 30th 2010
I further worked on the Idea-section at cohomology, expanding and polishing here and there.
Hit "see changes" to see what I did, precisely: changes (additions, mostly) concern mainly the part on nonabelian cohomology, and then at the end the part about twisted and differential cohomology.
by the way, what's your all opinion about that big inset by Jim Stasheff following the Idea section, ended by Toby's query box? I think we should remove this.
This is really essentially something I once wrote on my private web. Jim added some sentences to the first paragraph. Possibly he even meant to add this to my private web and by accident put it on the main Lab. In any case, that part is not realy fitting well with the flow of the entry (which needs improvement in itself) and most of the information is repeated anyway. I am pretty sure Jim won't mind if we essentially remove this. We could keep a paragraph that amplifies the situation in Top a bit, in an Examples-section.
What do you think?
- Discussion Type
- discussion topicon structured (oo,1)-topoi
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by zskoda
- Last Active Jan 29th 2010
<p>Since Mike's thread <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=679&page=1">questions on structured (oo,1)-topos</a> got a bit highjacked by general oo-stack questions, I thought I'd start this new thread to announce attempted answers:</p> <p>Mike had rightly complained in a query box that a "remark" of mine in which I had meant to indicate the intuitive meaning of the technical condition on an (oo,1)-structure sheaf had been "ridiculous".</p> <p>But that condition is important, and important to understand. I have now removed the nonsensical paragraph and Mike's query box complaining about it, inserted a new query box saying "second attempt" and then spelled out two archetypical toy examples in detail, that illustrate what's going on.</p> <p>The second of them can be found in StrucSp itself, as indicated. It serves mainly to show that an ordinary ringed space has a structure sheaf in the sense of structured oo-toposes precisely if it is a <a href="https://ncatlab.org/nlab/show/locally+ringed+space">locally ringed space</a>.</p> <p>But to try to bring out the very simple geometry behind this even better, I preceded this example now by one where a structure sheaf just of continuous functions is considered.</p> <p>Have a look.</p>
- Discussion Type
- discussion topiccosimplicial simplicial abelian groups and rings
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Jan 28th 2010
can anyone point me to some useful discussion of cosismplicial simplicial abelian groups
![\Delta \to [\Delta^{op}, Ab] \Delta \to [\Delta^{op}, Ab]](/extensions/vLaTeX/cache/latex_d1cc8ee3ed1bc3649a9309085cdbd8e6.png)
and cosimplicial simplicial rings
![\Delta \to [\Delta^{op}, CRing] \Delta \to [\Delta^{op}, CRing]](/extensions/vLaTeX/cache/latex_5d63c4f0c914aa3a558311cfc687015e.png)
I guess there should be a Dold-Kan correspondence relating these to unbounded (co)chain complexes (that may be nontrivial both in positive as well as in negative degree). I suppose it's kind of straightforward how this should work, but I'd still ike to know of any literature that might discuss this. Anything?
- Discussion Type
- discussion topicbigrading on cohomology
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 28th 2010
I expanded the section Gradings at cohomology. Made three sub-paragraphs:
integer grading
bigrading
exoctic grading
using the kind of insights that we were discussing recently in various places.
I also put in a query box where I wonder about a nice way to define a Chern character construction for general oo-stack oo-toposes.
- Discussion Type
- discussion topicCoo-rings
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by zskoda
- Last Active Jan 27th 2010
added an interesting reference by Kriegl and Michor to generalized smooth algebra, kindly pointed out by Thomas Nikolaus:
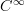 -algebras from the functional analyytic point of view
-algebras from the functional analyytic point of viewAlso added some other references.
- Discussion Type
- discussion topicBrown's Abstract Homotopy Theory and Generalized Sheaf Cohomology
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 25th 2010
I completely rewrote BrownAHT
same message as before, but I think I could say it much better now
- Discussion Type
- discussion topicde Rham space as derived free loop space
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 24th 2010
added a quick mention of the relation between deRham space and derived free loop space object to derived stack and Hochschild cohomology, pointing to this reference here for all the details
B. Toen, G. Vezzosi,
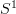 -Equivariant simplicial algebras and de Rham theory http://arxiv.org/abs/0904.3256
-Equivariant simplicial algebras and de Rham theory http://arxiv.org/abs/0904.3256more later.
- Discussion Type
- discussion topicrelative cohomology
- Category Latest Changes
- Started by Urs
- Comments 9
- Last comment by TobyBartels
- Last Active Jan 23rd 2010
this MO question on relative cohomology made me create an entry with an attempt to give the fully general abstract definition in the spirit of the discussion at cohomology
a very stubby note is now at relative cohomology
this clearly needs more development, but I think the basic idea is obvious
- Discussion Type
- discussion topicmotivic cohomology as stable oo-stack cohomology
- Category Latest Changes
- Started by Urs
- Comments 12
- Last comment by Urs
- Last Active Jan 21st 2010
I added to motivic cohomology the definition of motivic cohomology in terms of connected components of hom spaces in (the homotopy stabilization of) the (oo,1)-topos of oo-stacks on the Nisnevich site.
This is now the section Homotopy localization of the (oo,1)-topos on Nis.
Probably Zoran mentioned this before, without me getting it. Now I get it, and I like it a lot. This is the kind of nice formulation of motivic cohomology that one would expect from the point of view that is expressed at cohomology:
in fact, really a priori one should consider nonabelian motivic cohomology, by considering genuine oo-stacks on Nis, without stabilizing. One could consider differential Motivic cohomology by not retricting attention to the homotopy localization .
- Discussion Type
- discussion topichypersimplex
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Jan 21st 2010
I entered hypersimplex, which is a tip of an important iceberg in stable category business, I hope we can continue expanding the topic and do osme research on it.
- Discussion Type
- discussion topicinterval object: dendroidal version of path groupoid
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 19th 2010
at interval object we have a section that discusses how in a category with interval object for every object there are various incarnations of its "path groupoid".
We had had two such incarnations there: the first one discusses the structure of a Trimble n-category on this "path groupoid", the second one the structure of a simplicial set.
I want one more such incarnation: the structure of a planar dendroidal set.
A proposal for how that should work I have now typed in the new section titled currently Fundamental little 1-cubes space induced from an interval.
(This section title is bad, I need to think of something better...)
Eventually I want to see if this can be pushed to constitute the necessary ingredients for a "May recognition principle" in a general oo-stack oo-topos: over a site C with interval object, I want for each k a dendroidal presheaf that encodes something like the C-parameterized little k-cubes operad, which should act on k-fold loop oo-stacks on C.
That's the motivation, at least.
- Discussion Type
- discussion topicquasicoherent oo-stack
- Category Latest Changes
- Started by Urs
- Comments 10
- Last comment by Urs
- Last Active Jan 18th 2010
I started quasicoherent infinity-stack. Currently all this contains is a summary of some central definitions and propositions in Toen/Vezzosi's work. I tried to list lots of direct pointers to page and verse, as their two articles tend to be a bit baroque as far as notation and terminology is concerned.
This goes parallel with the blog discussion here.
In the process I also created stubs for SSet-site and model site. These are terms by Toen/Vezzosi, but I think these are obvious enough concepts that deserve an entry of their own. Eventually we should also have one titled "(oo,1)-site", probably, that points to these as special models.
- Discussion Type
- discussion topicsmooth natural numbers
- Category Latest Changes
- Started by Urs
- Comments 27
- Last comment by Urs
- Last Active Jan 18th 2010
created an entry smooth natural numbers
I tried to extract there the fundamental mechanism that makes the "nonstandard natural numbers" in Moerdijk-Reyes Models for Smooth Infinitesimal Analysis tick. In their book the basic idea is a bit hidden, but in fact it seems that it is a very elementary mechanism at work. I try to describe that at the entry. Would be grateful for a sanity check from topos experts.
I find it pretty neat how the sequences of numbers used to represent infinite numbers in nonstandard analysis appears (as far as I understand) as generalized elements of a sheaf in a sheaf topos here.
- Discussion Type
- discussion topicFredholm operator and K-theory
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 15th 2010
I noticed that we have an entry Fredholm operator. I added a very brief remark on the space of Fredholm operators as a classifying space for topological K-theory , and added there a very brief link back.
eventually, of course, it would be nice to add some details.
(also added sections and a toc).
- Discussion Type
- discussion topiclecture notes
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by Urs
- Last Active Jan 15th 2010
I once again can't enter the edit pages. So this here is just to remind myself:
I just discovered that the lecture notes for the Barcelona school a while ago are in fact online available, here:
Advanced Course on Simplicial Methods in Higher Categories
This should have been out as a book already, but keeps being delayed. It contains three important lectures, that we should link to from the respective entries:
Joyal's book on quasicategories
Moerdijk's book on dendroidal sets
Toen's lectures on simplicial presheaves
- Discussion Type
- discussion topicCategory Theory Problem on Right Adjoints
- Category Latest Changes
- Started by yellsap
- Comments 3
- Last comment by TobyBartels
- Last Active Jan 15th 2010
- How can I upload a document with diagrams that people can view the problem.
- Discussion Type
- discussion topicNew page: [[relative point of view]]
- Category Latest Changes
- Started by TobyBartels
- Comments 4
- Last comment by zskoda
- Last Active Jan 14th 2010
I started relative point of view based on material in the pages that link to it.
- Discussion Type
- discussion topicweighted join of quasi-categories
- Category Latest Changes
- Started by domenico_fiorenza
- Comments 12
- Last comment by Mike Shulman
- Last Active Jan 14th 2010
- in order to discuss weighted limits in my revision of limits, I introduced a stubby notion of weighted join of quasi-categories. The construction and the subsequent notion of weighted limit seem quite natural, but everithing now seems too simple, so I fear to have completely misunderstood the notion of weighted limit.. :(
could anybody give a look?
- Discussion Type
- discussion topicSullivan differential forms
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 13th 2010
- Discussion Type
- discussion topiccocycle
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Jan 11th 2010
started an entry cocycle to go along with the entry cohomology, motivated from my discussion with Mike on the blog here
I mention the possible terminology suggeestion of "anamorphisms" for cocycles there, and added a link to it from anafunctor.
- Discussion Type
- discussion topicWhitehead tower
- Category Latest Changes
- Started by Guest
- Comments 19
- Last comment by domenico_fiorenza
- Last Active Jan 10th 2010
- started Whitehead tower, plus some speculative comments on versions using higher categories.
-David Roberts
- Discussion Type
- discussion topicinternal oo-groupoid
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by domenico_fiorenza
- Last Active Jan 9th 2010
I found the discusssion at internal infinity-groupoid was missing some perspectives
I made the material originally there into one subsection called
- Kan complexes in an ordinary category
and added two more subsections
Kan complexes in an (oo,1)-category
Internal strict oo-groupoids .
The first of the two currently just points to the other relevant entry, which is groupoid object in an (infinity,1)-category, the second one is currently empty.
But I also added a few paragraphs in an Idea section preceeding everything, that is supposed to indicate how things fit together.
- Discussion Type
- discussion topic(infinity,2)-category
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 8th 2010
added to (infinity,2)-category a section models for the (oo,1)-category of all (oo,2)-categories
I also added (infinity,2)-category and Theta-space to the floating TOC
- Discussion Type
- discussion topic2-fibration at codomain fibration
- Category Latest Changes
- Started by Guest
- Comments 3
- Last comment by zskoda
- Last Active Jan 8th 2010
- Comment at codomain fibration about the suggested categorification, Cat^2 --> Cat. I personally don't think we've got to the bottom of what a 2-fibration is, with the possible exception of Igor Bakovic.
David Roberts
- Discussion Type
- discussion topicEilenberg–Mac Lane shenanigans
- Category Latest Changes
- Started by TobyBartels
- Comments 3
- Last comment by Urs
- Last Active Jan 8th 2010
I've just discovered that, from back in the days before redirects, we have two versions of Eilenberg-Mac Lane space. I have now combined them, by brute force; I'll leave it to Urs to make it look nice.
- Discussion Type
- discussion topicuniray group
- Category Latest Changes
- Started by Urs
- Comments 9
- Last comment by zskoda
- Last Active Jan 7th 2010
stubby stub for unitary group
- Discussion Type
- discussion topicdifferential cohomology - nonabelian case
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Jan 7th 2010
started adding a detailed "Idea" section to the page differential cohomology - nonabelian case on my personal web
currently this consists of the section The classical case of U-principal bundles and revolves around an abstract-nonsense interpretation of the Chern character
so this is in parts to be read as one more contribution in my discussion, elsewhere, with Domenico.
- Discussion Type
- discussion topicQuadratic Functions in Geometry, Topology,and M-Theory
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 7th 2010
created reference entry on Quadratic Functions in Geometry, Topology,and M-Theory, the fundamental article on differential cohomology.
- Discussion Type
- discussion topicnon-canonical isomorphisms
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Jan 7th 2010
I added some remarks regarding Steve Lack's paper of that name to biproduct and distributive category.
- Discussion Type
- discussion topicover quasi-categories
- Category Latest Changes
- Started by domenico_fiorenza
- Comments 5
- Last comment by TobyBartels
- Last Active Jan 6th 2010
- I've modified over quasi-categories in my personal area, upgrading from Hom-Sets to Hom-Spaces (i.e. infinity-categories of morphisms). This seems to simplify a lot the definition, and to make the connection with limits clearer. I'll wait for your comments before moving (in case they are positive) the version from my area to the main lab.
two technical questions:
i) how do i remove a page from my area (that's what I'd do after moving its content on the main lab)
ii) there's a link to over quasi-categories on the page Domenico Fiorenza, but it seems not to work, and I am missing the problem with it
- Discussion Type
- discussion topicrn-Simons gerbe
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 6th 2010
stub for Chern-Simons gerbe
- Discussion Type
- discussion topicSimons-Sullivan structured bundle
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 6th 2010
created Simons-Sullivan structured bundle
eventually I want to move the discussion currently in a subsection at differential K-theory to this entry
- Discussion Type
- discussion topicspace
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by zskoda
- Last Active Jan 5th 2010
In search for a more independent existence of the general abstract notes "Notions of Space" that were still bundled in the "talk notes"-page A Survey of Elliptic Cohomology - the derived moduli stack of derived elliptic curves I copied the material to the entry space.
- Discussion Type
- discussion topichomotopy n-type
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 5th 2010
John Baez added a query box to homotopy n-type
- Discussion Type
- discussion topicDifferential Graded (Noncommutative) Algebra of Whitney Forms
- Category Latest Changes
- Started by Eric
- Comments 2
- Last comment by Urs
- Last Active Jan 4th 2010
I am pretty happy with what I just wrote at
Modified Wedge Product (ericforgy)
I proposed the idea years ago, but only now found a voice to express it in way that I think might resonate with others.
Basically, we have differential forms
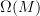 and cochains
and cochains 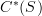 and maps:
and maps: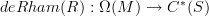
and
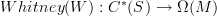
that satisfy
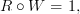 <br/>
<br/> <br/>
<br/>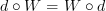 , and
, and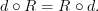
However, one thing that has always bugged me is that these maps do not behave well with products. The wedge product in
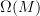 is graded commutative "on the nose" and the cup product in
is graded commutative "on the nose" and the cup product in 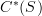 is not graded commutative "on the nose", but is graded commutative when you pass to cohomology.
is not graded commutative "on the nose", but is graded commutative when you pass to cohomology.The image of
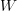 is called the space of "Whitney forms" and has been used for decades by engineers in computational physics due to the fact that Whitney forms provide a robust numerical approximation to smooth forms since the exterior derivative commutes with the Whitney map and we get exact conservation laws (cohomology is related to conserved quantities in physics).
is called the space of "Whitney forms" and has been used for decades by engineers in computational physics due to the fact that Whitney forms provide a robust numerical approximation to smooth forms since the exterior derivative commutes with the Whitney map and we get exact conservation laws (cohomology is related to conserved quantities in physics).One thing that always bugged me about Whitney forms is that they are not closed as an algebra under the ordinary wedge product, i.e. the wedge product of two Whitney forms is not a Whitney form. Motivated by this I proposed a new "modified wedge product" that turned Whitney forms into a graded differential algebra.
Now although in grade 0, Whitney forms commute, Whitney 0-forms and Whitney 1-forms do not commute except in the continuum limit where the modified wedge product converges to the ordinary wedge product and Whitney forms converge to smooth forms.
I think this might be a basis for examining the "cochain problem" John talked about in TWFs Week 288.
To the best of my knowledge, this is the first time a closed algebra of Whitney forms has been written down, although I would not be completely surprised if it is written down in some tome from 100 years ago (which I guess would be hard since it would predate Whitney).
Another nice thing about the differential graded noncommutative algebra of Whitney forms is that they are known to converge to smooth forms with sufficiently nice simplicial refinements (a kind of nice continuum limit) and you have true morphisms from the category of Whitney forms to the category of cochains (or however you want to say it). In other words, I believe the arrow theoretic properties of Whitney forms will be nicer than those of smooth forms.
- Discussion Type
- discussion topicregular and exact completion
- Category Latest Changes
- Started by Mike Shulman
- Comments 8
- Last comment by Todd_Trimble
- Last Active Jan 4th 2010
Started writing regular and exact completion.
- Discussion Type
- discussion topicderivation and Kähler differential
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by John Baez
- Last Active Jan 3rd 2010
I expanded derivation a little:
gave the full definition with values in bimodules and added to the examples a tiny little bit on examples for this case.
I think I also corrected a mistake in the original version of the definition: the morphism
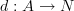 is of course not required to be a module homomorphism (well, it is, but over the underlying ground ring, not over
is of course not required to be a module homomorphism (well, it is, but over the underlying ground ring, not over  ).
).At Kähler differential I just polished slightly, adding a few words and links in the definition and adding sections. I don't really have time for this derivations/Kähler stuff at the moment. Am hoping that those actively talki9ng about this on the blog will find the time to archive their stable insights at this entry.
- Discussion Type
- discussion topicfolk model structure on Cat
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Jan 1st 2010
I started writing folk model structure on Cat with an explicit summary of the construction, and a description of how it can be modified to work if you assume only COSHEP. I feel like there should also be a "dual" model structure assuming some other weakening of choice, in which all categories are cofibrant and the fibrant objects are the "stacks", but I haven't yet been able to make it come out right.
- Discussion Type
- discussion topic[[weak factorization system on Set]]
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Jan 1st 2010
Mike Shulman wrote weak factorization system on Set, which is very nice.
- Discussion Type
- discussion topicanafunctors
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Jan 1st 2010
Motivated by this question on MO, created weak factorization system on Set and added some comments about size questions to anafunctor.
- Discussion Type
- discussion topictopos
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Mike Shulman
- Last Active Dec 30th 2009
- Discussion Type
- discussion topicoo-Lie differentiation and integration
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Dec 30th 2009
expanded the Idea-section at schreiber:oo-Lie differentiation and integration and polished the section of oo-Lie diffeentiation somewhat, following the blog discussion here
- Discussion Type
- discussion topicThose evil †-categories
- Category Latest Changes
- Started by TobyBartels
- Comments 5
- Last comment by Mike Shulman
- Last Active Dec 30th 2009
Discussion has spilt from the
categoriesmailing list into evil.
- Discussion Type
- discussion topicQuestion on Grothendieck fibrations.
- Category Latest Changes
- Started by TobyBartels
- Comments 2
- Last comment by Mike Shulman
- Last Active Dec 30th 2009
Sridhar Ramesh has one at Grothendieck fibration.
- Discussion Type
- discussion topicGrothendieck fibration+topological K-theory
- Category Latest Changes
- Started by Guest
- Comments 6
- Last comment by domenico_fiorenza
- Last Active Dec 28th 2009
- At Grothendieck fibration I wonder if we can make the definition less evil than the non-evil version there, with applications to Dold fibrations. Also the insertion of a necessary adjective at topological K-theory.
-David Roberts
- Discussion Type
- discussion topicAlgebraic categories
- Category Latest Changes
- Started by TobyBartels
- Comments 14
- Last comment by Mike Shulman
- Last Active Dec 24th 2009
I started algebraic category, with a note also at monadic adjunction.
- Discussion Type
- discussion topicoo-limits - contents
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by TobyBartels
- Last Active Dec 24th 2009
created infinity-limits - contents and added it as a toc to relevant entries
(maybe I shoulod have titled the page differently, but it doesn't matter much for a toc)
- Discussion Type
- discussion topicbutterfly
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Dec 23rd 2009
started expanding butterfly
also butterfly diagrams at crossed profunctor
- Discussion Type
- discussion topicdeRham theorem for oo-Lie groupoids
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 22nd 2009
filled a gap in deRham theorem for oo-Lie groupoids on my personal web.
But I need to sleep over this...
- Discussion Type
- discussion topiccontractible objects in a lined topos
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Dec 22nd 2009
created a section Contractible objects at lined topos.
This introduces and discusses a bit a notion of objects being contractible with respect to a specified line object (maybe the section deserves to be at interval object instead, not sure).
This notion is something I made up, so review critically. I am open for suggestions of different terminology. The concept itself, simple as it is (though not entirely trivial), I need for the discussion of path oo-groupoids of oo-stacks on my personal web:
if a lined Grothendieck topos
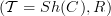 is such that all representable objects are contractible with respect to the line object
is such that all representable objects are contractible with respect to the line object 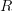 , then the path oo-groupoid functor
, then the path oo-groupoid functor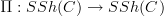
on simplicial sheaves, which a priori is only a Qulillen functor of oo-prestacks, enhances to a Quillen functor of oo-stacks (i.e. respects the local weak equivalences).
- Discussion Type
- discussion topicshape fibration
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Dec 22nd 2009
An incomplete introduction to shape fibration and a related bio entry Sibe Mardesic.
- Discussion Type
- discussion topicBeck–Chevalley
- Category Latest Changes
- Started by TobyBartels
- Comments 7
- Last comment by zskoda
- Last Active Dec 22nd 2009
Somebody wrote quite the stub at Beck-Chevalley_Condition; I fixed the name but didn't mess with it otherwise. It seems to have appeared (properly named) on Mike's web too, all by the AnonymousCoward.
- Discussion Type
- discussion topicspace and quantity
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 21st 2009
Added to the Idea section at space and quantity a short paragraph with pointers to the (oo,1)-categorical realizations. (Parallel to the blog discussion here)