nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
- Discussion Type
- discussion topicdouble dimensional reduction
- Category Latest Changes
- Started by Urs
- Comments 16
- Last comment by Urs
- Last Active Apr 5th 2024
am in the process of adding some notes on how the D=5 super Yang-Mills theory on the worldvolume of the D4-brane is the double dimensional reduction of the 6d (2,0)-superconformal QFT in the M5-brane.
started a stubby double dimensional reduction in this context and added some first further pointers and references to M5-brane, to D=5 super Yang-Mills theory and maybe elsewhere.
But this still needs more details to be satisfactory, clearly.
- Discussion Type
- discussion topicalgebraic K-theory
- Category Latest Changes
- Started by Tim_Porter
- Comments 50
- Last comment by Urs
- Last Active Apr 5th 2024
I have started on a revision of algebraic K-theory. The old version launched straight into a particular nPOV, which really just summarised the Blumberg et al paper, and did not mention any of the other ideas in the area. At present I have just put in some historical stuff, but given the importance of the subject e.g. in modern C*-algebra the page needs a lot more work.
- Discussion Type
- discussion topicAdS-CFT in condensed matter physics
- Category Latest Changes
- Started by Urs
- Comments 23
- Last comment by Urs
- Last Active Apr 5th 2024
- Discussion Type
- discussion topicchiral perturbation theory
- Category Latest Changes
- Started by Urs
- Comments 21
- Last comment by Urs
- Last Active Apr 5th 2024
- Discussion Type
- discussion topichyperdoctrine
- Category Latest Changes
- Started by nLab edit announcer
- Comments 3
- Last comment by nLab edit announcer
- Last Active Apr 4th 2024
- Discussion Type
- discussion topictangent category
- Category Latest Changes
- Started by Urs
- Comments 9
- Last comment by nLab edit announcer
- Last Active Apr 4th 2024
created tangent category
in order to have a place where to keep just details on the purely 1-categorical "shadow" of tangent (infinity,1)-category.
- Discussion Type
- discussion topicduality between M/F-theory and heterotic string theory
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by Urs
- Last Active Apr 4th 2024
- Discussion Type
- discussion topicn-plectic vector space
- Category Latest Changes
- Started by perezl.alonso
- Comments 1
- Last comment by perezl.alonso
- Last Active Apr 3rd 2024
definition of -lagrangian subspaces from
- Manuel de León, David Martín de Diego, Aitor Santamaría-Merino. Tulczyjew’s triples and lagrangian submanifolds in classical field theories (2003). (arXiv:math-ph/0302026).
should also include Definition 3.18 from that paper (-lagrangian submanifolds) somewhere but there are at least two different relevant entries (multisymplectic geometry, n-plectic geometry).
- Discussion Type
- discussion topicquasi-topological space
- Category Latest Changes
- Started by DavidRoberts
- Comments 3
- Last comment by ʇɐ
- Last Active Apr 3rd 2024
- Discussion Type
- discussion topicco-relation
- Category Latest Changes
- Started by mattecapu
- Comments 5
- Last comment by Urs
- Last Active Apr 3rd 2024
- Discussion Type
- discussion topicquantum harmonic oscillator
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 3rd 2024
added pointer to today’s
- Alexander D. Popov, Quantum charges of harmonic oscillators [arXiv:2404.01756]
- Discussion Type
- discussion topicLiouville theory
- Category Latest Changes
- Started by Urs
- Comments 12
- Last comment by Urs
- Last Active Apr 3rd 2024
started something stubby at Liouville theory, for the moment just so as to record some references and provide for a minimum of cross-links (e.g. with Chern-Simons gravity).
(also created a stub for quantum Teichmüller theory in the course of this, but nothing there yet except a pointer to reviews)
- Discussion Type
- discussion topicLachezar S. Georgiev
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 3rd 2024
- Discussion Type
- discussion topicLaughlin wavefunctions as conformal blocks -- references
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Apr 3rd 2024
creating here a bare list of references, to be
!include-ed into the References-list at relevant entries (notably at Laughlin wavefunction and at conformal block)
- Discussion Type
- discussion topiclist of category theory papers that never appeared
- Category Latest Changes
- Started by varkor
- Comments 9
- Last comment by varkor
- Last Active Apr 2nd 2024
- Discussion Type
- discussion topicPCT theorem
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Apr 2nd 2024
added missing pointer to
- Raymond F. Streater, Arthur S. Wightman, PCT, Spin and Statistics, and All That, Princeton University Press (1989, 2000) [ISBN:9780691070629, jstor:j.ctt1cx3vcq]
and pointer to:
- Franco Strocchi, §4.3 in: An Introduction to Non-Perturbative Foundations of Quantum Field Theory, Oxford University Press (2013) [doi:10.1093/acprof:oso/9780199671571.001.0001]
- Discussion Type
- discussion topicMetamath
- Category Latest Changes
- Started by nLab edit announcer
- Comments 6
- Last comment by nLab edit announcer
- Last Active Apr 2nd 2024
- Discussion Type
- discussion topicM. D. Pollock
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 2nd 2024
- Discussion Type
- discussion topicDirac equation
- Category Latest Changes
- Started by Dmitri Pavlov
- Comments 3
- Last comment by Urs
- Last Active Apr 2nd 2024
- Discussion Type
- discussion topiccurved spacetime
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 2nd 2024
- Discussion Type
- discussion topicmonadic functor
- Category Latest Changes
- Started by Alec Rhea
- Comments 17
- Last comment by nLab edit announcer
- Last Active Apr 2nd 2024
The link for ’equivalent’ at the top redirected to natural isomorphism which (as I understand it) is the correct 1-categorical version of an equivalence of functors, but this initially lead me to believe that a functor was monadic iff it was naturally isomorphic to a forgetful functor from the Eilenberg-Moore category of a monad on its codomain, which would mean that the domain of the functor was literally the Eilenberg-Moore category of some adjunction since natural isomorphism is only defined for parallel functors.
- Discussion Type
- discussion topicconnection on a smooth principal infinity-bundle
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by Urs
- Last Active Apr 2nd 2024
I have renamed the entry formerly called (and still redirecting) “connection on a principal infinity-bundle” into connection on a smooth principal infinity-bundle.
I will now start with bringing that entry into shape.
In the same vein I have renamed the entry formerly titled (and still redirecting) “infinity-Chern-Weil theory” into Chern-Weil theory in Smooth∞Grpd.
This way things are set up well for when the legions of students arrive who will do all the analogous discussion in other cohesive -toposes such as , as well as the derived version of all of these. ;-)
- Discussion Type
- discussion topicEudoxus
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 2nd 2024
- Discussion Type
- discussion topicEudoxus real number
- Category Latest Changes
- Started by Todd_Trimble
- Comments 8
- Last comment by nLab edit announcer
- Last Active Apr 1st 2024
Wrote an article Eudoxus real number, a concept due to Schanuel.
- Discussion Type
- discussion topicCayley form
- Category Latest Changes
- Started by Urs
- Comments 15
- Last comment by Urs
- Last Active Apr 1st 2024
- Discussion Type
- discussion topicquantization via the A-model
- Category Latest Changes
- Started by nLab edit announcer
- Comments 3
- Last comment by perezl.alonso
- Last Active Apr 1st 2024
- Discussion Type
- discussion topictopological twist
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by perezl.alonso
- Last Active Apr 1st 2024
added pointer to Elliott-Safronov 18
- Discussion Type
- discussion topicFukaya category
- Category Latest Changes
- Started by Urs
- Comments 7
- Last comment by perezl.alonso
- Last Active Apr 1st 2024
added pointer to section 7.5 of
- Fernando Marchesano, Intersecting D-brane Models (arXiv:hep-th/0307252)
- Discussion Type
- discussion topicadjoint triple
- Category Latest Changes
- Started by Mike Shulman
- Comments 21
- Last comment by Urs
- Last Active Apr 1st 2024
I added some references to adjoint triple for the folklore theorem about fully faithful adjoint triples.
- Discussion Type
- discussion topicreflective subcategory
- Category Latest Changes
- Started by Urs
- Comments 35
- Last comment by Urs
- Last Active Mar 31st 2024
edited reflective subcategory and expanded a bit the beginning
- Discussion Type
- discussion topicK3 surface
- Category Latest Changes
- Started by Urs
- Comments 8
- Last comment by Urs
- Last Active Mar 31st 2024
- Discussion Type
- discussion topicuniverse in a topos
- Category Latest Changes
- Started by Thomas Holder
- Comments 6
- Last comment by Urs
- Last Active Mar 30th 2024
- Discussion Type
- discussion topicepsilon-number
- Category Latest Changes
- Started by Mike Shulman
- Comments 4
- Last comment by nLab edit announcer
- Last Active Mar 30th 2024
Created ε-number.
- Discussion Type
- discussion topicgeometric realization of categories
- Category Latest Changes
- Started by nLab edit announcer
- Comments 8
- Last comment by nLab edit announcer
- Last Active Mar 30th 2024
- Discussion Type
- discussion topicNiccolò Cribiori
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 29th 2024
- Discussion Type
- discussion topicswampland cobordism conjecture -- references
- Category Latest Changes
- Started by Urs
- Comments 8
- Last comment by Urs
- Last Active Mar 29th 2024
This is a bare list of references, to be
!include-ed into relevant entries, such as at swampland and 24 branes transverse to K3, for ease of cross-linking and updating.I am taking the liberty of including a pointer to our upcoming M/F-Theory as Mf-Theory which has some details on a precise version of the conjecture and a proof (from Hypothesis H).
- Discussion Type
- discussion topicabc conjecture
- Category Latest Changes
- Started by zskoda
- Comments 61
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
- Discussion Type
- discussion topicKirti Joshi
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
brief
category:people-entry for satisfying links now requested at p-adic Teichmüller theory
- Discussion Type
- discussion topicmanifold calculus
- Category Latest Changes
- Started by David_Corfield
- Comments 3
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
Added to references:
Brian Munson, Introduction to the manifold calculus of Goodwillie-Weiss (arXiv:1005.1698)
Thomas Willwacher, Configuration spaces of points and real Goodwillie-Weiss calculus, talk at Isaac Newton Institute, 2018.
- Discussion Type
- discussion topichomotopy coherent nerve
- Category Latest Changes
- Started by Urs
- Comments 42
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
added to homotopy coherent nerve two diagrams in the section Examples and illustrations that are supposed to illustrate the hom-SSets of the simplicial category on
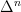
- Discussion Type
- discussion topicsimplicial localization
- Category Latest Changes
- Started by Tim_Porter
- Comments 10
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
Someone deleted the contents of the entry simplicial localization on th 4 April, then another reinstated it on the 5th. Curious!
- Discussion Type
- discussion topiclocalization of an (infinity,1)-category
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
added pointer to:
- Marco Vergura, Localization Theory in an Infinity Topos, 2019 (pdf, ir.lib.uwo.ca:etd/6257)
- Discussion Type
- discussion topicKensuke Arakawa
- Category Latest Changes
- Started by nLab edit announcer
- Comments 1
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
- Discussion Type
- discussion topiccomplete Segal space
- Category Latest Changes
- Started by Urs
- Comments 16
- Last comment by nLab edit announcer
- Last Active Mar 29th 2024
added to complete Segal space a discussion of what an ordinary category looks like when regarded as a complete Segal space.
(This is meant to be pedagogical, therefore the recollection of all the basics at the beginning.)
- Discussion Type
- discussion topicBlakers-Massey theorem
- Category Latest Changes
- Started by Urs
- Comments 34
- Last comment by varkor
- Last Active Mar 28th 2024
stub for Blakers-Massey theorem. Need to add more references…
- Discussion Type
- discussion topicSteenrod algebra
- Category Latest Changes
- Started by Urs
- Comments 23
- Last comment by J-B Vienney
- Last Active Mar 28th 2024
some basics at Steenrod algebra
- Discussion Type
- discussion topiccobordism category
- Category Latest Changes
- Started by Urs
- Comments 10
- Last comment by Dmitri Pavlov
- Last Active Mar 28th 2024
added this pointer on the homotopy groups of the embedded cobordism category:
Marcel Bökstedt, Anne Marie Svane, A geometric interpretation of the homotopy groups of the cobordism category, Algebr. Geom. Topol. 14 (2014) 1649-1676 (arXiv:1208.3370)
Marcel Bökstedt, Johan Dupont, Anne Marie Svane, Cobordism obstructions to independent vector fields, Q. J. Math. 66 (2015), no. 1, 13-61 (arXiv:1208.3542)
- Discussion Type
- discussion topiclagrangian submanifold
- Category Latest Changes
- Started by nLab edit announcer
- Comments 10
- Last comment by perezl.alonso
- Last Active Mar 28th 2024
Anel and Catren in their introduction to New Spaces in Physics claim that Lagrangian submanifolds are category-theoretic “points” of a symplectic manifold, morphisms from the trivial symplectic manifold in Weinstein’s symplectic category.
Is this accurate?
Anonymous
- Discussion Type
- discussion topictopological group
- Category Latest Changes
- Started by Todd_Trimble
- Comments 31
- Last comment by nLab edit announcer
- Last Active Mar 28th 2024
The entry on topological group could stand more work, but I added some stuff on the uniform structure, in particular the proposition that for group homomorphisms , continuity at a single point guarantees uniform continuity over all of . The proof is follow-your-nose, of course.
What we really need is an entry Haar measure. I’ll get started on that soon.
- Discussion Type
- discussion topicAustralian Category Seminar
- Category Latest Changes
- Started by varkor
- Comments 9
- Last comment by AlexanderCampbell
- Last Active Mar 28th 2024
- Discussion Type
- discussion topiccoverage
- Category Latest Changes
- Started by IngoBlechschmidt
- Comments 18
- Last comment by Urs
- Last Active Mar 28th 2024
At coverage, I just made the following change: Where the sheaf condition previously read
it now uses the variable names “” and “” instead of “” and “”:
I’m announcing this almost trivial change because I’d like to invite objections, in which case I’d rollback that change and also would not go on to copy this change to related entries such as sheaf. There are two tiny reasons why I prefer the new variable names:
- It’s more symmetric. The previous notation unjustly favored “”.
- It’s slightly easier to infer the definition of the two maps. (I had a student who was briefly confused by the original notation.)
- Discussion Type
- discussion topicM-Theory and Mathematics
- Category Latest Changes
- Started by Urs
- Comments 17
- Last comment by Urs
- Last Active Mar 28th 2024
- Discussion Type
- discussion topicretract
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by J-B Vienney
- Last Active Mar 28th 2024
edited retract a little
- Discussion Type
- discussion topicdiscrete fibration
- Category Latest Changes
- Started by zskoda
- Comments 16
- Last comment by Dmitri Pavlov
- Last Active Mar 27th 2024
In discrete fibration I added a new section on the Street’s definition of a discrete fibration from to , that is the version for spans of internal categories. I do not really understand this added definition, so if somebody has comments or further clarifications…
- Discussion Type
- discussion topicmonoidal functor
- Category Latest Changes
- Started by Urs
- Comments 15
- Last comment by nLab edit announcer
- Last Active Mar 27th 2024
created (finally) lax monoidal functor (redirecting monoidal functor to that) and strong monoidal functor.
Hope I got the relation to 2-functors right. I remember there was some subtlety to be aware of, but I forget which one. I could look it up, but I guess you can easily tell me.
- Discussion Type
- discussion topicmonoidal category
- Category Latest Changes
- Started by Urs
- Comments 109
- Last comment by nLab edit announcer
- Last Active Mar 27th 2024
Todd,
when you see this here and have a minute, would you mind having a look at monoidal category to see if you can remove the query-box discussion there and maybe replace it by some crisp statement?
Thanks!
- Discussion Type
- discussion topicpro-étale morphism of schemes
- Category Latest Changes
- Started by nLab edit announcer
- Comments 2
- Last comment by nLab edit announcer
- Last Active Mar 27th 2024
- Discussion Type
- discussion topicBethe ansatz
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Mar 26th 2024
- Discussion Type
- discussion topicBlake Stacey
- Category Latest Changes
- Started by nLab edit announcer
- Comments 1
- Last comment by nLab edit announcer
- Last Active Mar 26th 2024
- Discussion Type
- discussion topicBott connection
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by zskoda
- Last Active Mar 26th 2024